解:(1)设抛物线的解析式为y=ax
2+bx+c
∵此抛物线经过点A(1,0)、B(3,0)、C(0,2)
∴a+b+c=0,9a+3b+c=0,c=3
∴a=1,b=-4,c=3
∴抛物线的解析式为y=x
2-4x+3
(2)过E作ED⊥AB于D,连接BE
设交点E(m,n)则AD=m-1,BD=3-m,DE=-n
∵AB为圆的直径
∴∠AEB=90°
∴∠EAB+∠ABE=90°
∵ED⊥AB
∴∠ADE=∠EDB=90°
∴∠DEB+∠ABE=90°
∴∠DEB=∠EAB
∴△ADE∽△EDB
∴

=
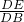
∴
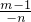
=
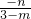
∴m
2-4m+3=-n
2又∵E(m,n)在抛物线y=x
2-4x+3
∴n=m
2-4m+3
∴n=-n
2∴n=-1或n=0(不合题意舍去)
∴m=2
∴该圆与抛物线交点坐标为(2,1)
(3)设当抛物线与圆相切时E(m,n),则O′E
2=(2-m)
2+(-n)
2∴r
2=(2-m)
2+(-n)
2又∵E(m,n)在抛物线y=x
2-4x+3
∴n=m
2-4m+3=(m-2)
2-1
∴r
2=(2-m)
2+((m-2)
2-1)
2∴(m-2)
4-(m-2)
2+1-r
2=0
∵当抛物线与圆相切时只有两个交点
∴m只有两个正数解
∵方程(m-2)
4-(m-2)
2+1-r
2=0中m-2的两个解均为正数
∴此方程的b
2-4ac=0
∴r=

∵当r=1时有三个交点
∴当0<r<

时无交点;
当r=

或r>1时有两个交点;
当r=1时有三个交点;
当

<r<1时有四个交点.
分析:(1)可根据A、B的坐标用交点式的二次函数通式来设这个二次函数,然后根据C的坐标来确定其解析式.
(2)可求E、F两点中任何一个的坐标,以E点为例,过E作ED⊥AB于D,连接BE,先设出E点的坐标,如E点的坐标为(m,n),可用m、n表示出AD、DE、BD的长,根据射影定理可得出DE
2=AD•DE,即可得出关于m、n的等量关系式,然后可依据E是抛物线上的点,将E的坐标代入抛物线的解析式中,可得出另外一个关于m、n的关系式,让这两个式子联立,即可求出m,n的值,也就得出E点的坐标.
(3)可先求出圆O′与抛物线相切时的圆的半径是多少.可设相切时,切点E的坐标为(m,n),可根据O′、E两点的坐标,求出O′E的长度,也就得出了半径的长,设半径为r,那么就得出了关于r、m、n的等量关系式.又有E是抛物线上的点,可将E的坐标代入抛物线的解析式中,得出关于m,n的等量关系式,然后联立两式即可得出关于、r的方程.已知了此时圆与抛物线相切,因此有两个切点.可根据根与系数的关系得出此时r的值.然后根据这个半径的值即可得出半径在不同的取值范围中,圆与抛物线的不同的位置关系,也就可得出了交点的个数.
点评:本题结合圆的知识考查了二次函数的综合应用,运用数形结合的方法进行解答是本题的基本思路.

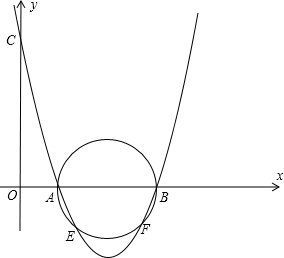 已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆. =
=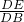 ∴
∴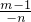 =
=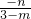
 ∵当r=1时有三个交点
∵当r=1时有三个交点 时无交点;
时无交点; 或r>1时有两个交点;
或r>1时有两个交点; <r<1时有四个交点.
<r<1时有四个交点.

 名校课堂系列答案
名校课堂系列答案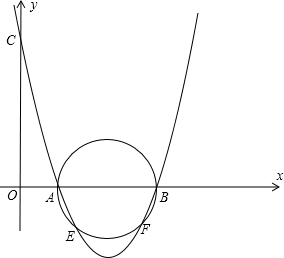 已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆. 如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.
如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.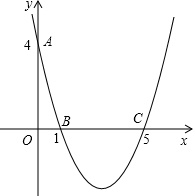 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.