
【题目】如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.

(1)求∠AGF的度数;
(2)连接DG,若AG=3、BG=2,求DG的长.
【答案】(1)∠AGF=60°;(2)DG=5.
【解析】
(1)根据等边三角形的性质得到AB=BC,∠ABC=∠C=60°,再根据三角形全等的判定方法可证得△ABE≌△BCF,则∠BAE=∠FBC,利用三角形外角性质得∠BGE=∠ABG+∠BAE,则∠BGE=∠ABG+∠FBC=∠ABC=60°,然后根据对顶角相等即可得到结论;
(2)延长GE至点H,使GH=GB,由于∠BGE=60°,根据等边三角形的判定得到△BGH为等边三角形,然后根据等边三角形的性质得到BG=BH=GH,∠GBH=60°,且AB=BD,∠ABD=60°,易得∠ABH=∠DBG,根据三角形全等的判定方法可证得△DBG≌△ABH(SAS),则DG=AH,即可得到DG=AG+BG.
(1)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
∵在△ABE和△BCF中,
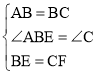 ,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠FBC,
∵∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°,
∴∠AGF=∠BGE=60°;
(2)证明:延长GE至点H,使GH=GB,如图,
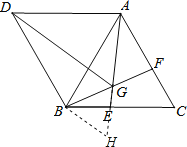
∵∠BGE=60°,
∴△BGH为等边三角形,
∴BG=BH=GH,∠GBH=60°,
∵△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∵∠ABH=∠GBH+∠ABG,∠DBG=∠ABD+∠ABG,
∴∠ABH=∠DBG,
∵在△DBG和△ABH中,
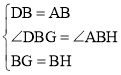 ,
,
∴△DBG≌△ABH(SAS),
∴DG=AH,
而AH=AG+GH,
∴DG=AG+BG,
∵AG=3,BG=2,
∴DG=5.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,在⊙O上取点D,连接CD,使得AC=CD,延长CD交直线AB于点E.
(1)求证:CD是⊙O的切线.
(2)若AC=2![]() ,AE=6.
,AE=6.
①求⊙O的半径.
②点M是优弧![]() 上的一个动点(不与B,D重合),求MD,MB及弧BD围成的阴影部分面积的最大值.
上的一个动点(不与B,D重合),求MD,MB及弧BD围成的阴影部分面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称轴图形△A1B1C1(不写画法);
点A1的坐标为 ;点B1的坐标为 ;点C1的坐标为 .
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB、AC为边向外作等边三角形△ABD与△ACE,线段BE交DC于点F,下列结论:①CD=BE;②FA平分∠BAC;③∠BFC=120°,④FA+FB=FD,其中正确有( )个.

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年4月22日是第49个世界地球日,今年的主题为“珍惜自然资源呵护美丽国土一讲好我们的地球故事”地球日活动周中,同学们开展了丰富多彩的学习活动,某小组搜集到的数据显示,山西省总面积为15.66万平方公里,其中土石山区面积约5.59万平方公里,其余部分为丘陵与平原,丘陵面积比平原面积的2倍还多0.8万平方公里.
(1)求山西省的丘陵面积与平原面积;
(2)活动周期间,两位家长计划带领若干学生去参观山西地质博物馆,他们联系了两家旅行社,报价均为每人30元.经协商,甲旅行社的优惠条件是,家长免费,学生都按九折收费;乙旅行社的优惠条件是,家长、学生都按八折收费.若只考虑收费,这两位家长应该选择哪家旅行社更合算?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴分别交于点A(﹣2,0),B(4,0),与y轴交于点C,点D是y轴负半轴上一点,直线BD与抛物线y=ax2+bx+3在第三象限交于点E(﹣4,y)点F是抛物线y=ax2+bx+3上的一点,且点F在直线BE上方,将点F沿平行于x轴的直线向右平移m个单位长度后恰好落在直线BE上的点G处.
(1)求抛物线y=ax2+bx+3的表达式,并求点E的坐标;
(2)设点F的横坐标为x(﹣4<x<4),解决下列问题:
①当点G与点D重合时,求平移距离m的值;
②用含x的式子表示平移距离m,并求m的最大值;
(3)如图2,过点F作x轴的垂线FP,交直线BE于点P,垂足为F,连接FD.是否存在点F,使△FDP与△FDG的面积比为1:2?若存在,直接写出点F的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购进一批足球,从商场了解到:一个A型足球和三个B型足球共需275元;三个A型足球和两个B型足球共需300元.
(1)列二元一次方程组解决问题:求一个A型足球和一个B型足球的售价各是多少元;
(2)若该学校准备同时购进这两种型号的足球共80个,并且A型足球的数量小于等于60个,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款![]() 元用来代理品牌服装的销售.已知该品牌服装进价每件
元用来代理品牌服装的销售.已知该品牌服装进价每件![]() 元,日销售
元,日销售![]() (件)与销售价
(件)与销售价![]() (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天
(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天![]() 元,每天应支付其它费用
元,每天应支付其它费用![]() 元.
元.

![]() 求日销售
求日销售![]() (件)与销售价
(件)与销售价![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
![]() 若暂不考虑还贷,当某天的销售价为
若暂不考虑还贷,当某天的销售价为![]() 元/件时,收支恰好平衡(收入
元/件时,收支恰好平衡(收入![]() 支出),求该店员工人数;
支出),求该店员工人数;
![]() 若该店只有
若该店只有![]() 名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com