
”¾ĢāÄæ”æČēĶ¼£¬Ķ¼Ļó£ØÕŪĻßABCDE£©ĆčŹöĮĖŅ»Ęū³µŌŚÄ³Ņ»Ö±ĻßÉĻµÄŠŠŹ»¹ż³ĢÖŠ£¬Ęū³µĄė³ö·¢µŲµÄ¾ąĄės£ØĒ§Ć×£©ŗĶŠŠŹ»Ź±¼ät£ØŠ”Ź±£©Ö®¼äµÄŗÆŹż¹ŲĻµ£¬øł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬øų³öĻĀĮŠĖµ·Ø£¬ĘäÖŠÕżČ·µÄĖµ·ØŹĒ£Ø””””£©

A. Ęū³µ¹²ŠŠŹ»ĮĖ120Ē§Ć× B. Ęū³µŌŚÕūøöŠŠŹ»¹ż³ĢÖŠĘ½¾łĖŁ¶ČĪŖ40Ē§Ć×
C. Ęū³µ·µ»ŲŹ±µÄĖŁ¶ČĪŖ80Ē§Ć×/Ź± D. Ęū³µ×Ō³ö·¢ŗó1.5Š”Ź±ÖĮ2Š”Ź±Ö®¼äĖŁ¶Č²»±ä
”¾“š°ø”æC
”¾½āĪö”æ·ÖĪö£ŗŗįÖį“ś±ķŹ±¼ä£¬×ŻÖį“ś±ķŠŠŹ»µÄĀ·³Ģ£¬¾Ż“ĖÅŠ¶ĻĻąÓ¦µÄĀ·³ĢŗĶŹ±¼ä¼“æÉ£®
Ļź½ā£ŗA”¢ÓÉĶ¼ĻóæÉŅŌ擳ö£¬×īŌ¶“¦µ½“ļ¾ąĄė³ö·¢µŲ120Ē§Ćד¦£¬µ«ÓÖ·µ»ŲŌµŲ£¬ĖłŅŌŠŠŹ»µÄĀ·³ĢĪŖ240Ē§Ć×£¬“ķĪ󣬲»·ūŗĻĢāŅā£»
B”¢Ę½¾łĖŁ¶ČĪŖ×ÜĀ·³Ģ”Ā×ÜŹ±¼ä£¬×ÜĀ·³ĢĪŖ240Ē§Ć×£¬×ÜŹ±¼äĪŖ4.5Š”Ź±£¬ĖłŅŌĘ½¾łĖŁ¶ČĪŖ240”Ā4.5”Ö53Ē§Ć×/Ź±£¬¹Ź“ķĪ󣬲»·ūŗĻĢāŅā£»
C”¢Ęū³µ·µ»ŲĖłÓƵď±¼äŹĒ1.5Š”Ź±£¬ŌņĘ½¾łĖŁ¶ČĪŖ£ŗ![]() =80£ØĒ§Ć×/Ź±£©£¬ÕżČ·£¬·ūŗĻĢāŅā£»
=80£ØĒ§Ć×/Ź±£©£¬ÕżČ·£¬·ūŗĻĢāŅā£»
D”¢Ęū³µ×Ō³ö·¢ŗó3Š”Ź±ÖĮ4.5Š”Ź±Ö®¼äŠŠŹ»µÄĖŁ¶Č²»±ä£¬¹Ź“ķĪ󣬲»·ūŗĻĢāŅā£»
¹ŹŃ”C£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
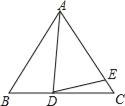
”¾ĢāÄæ”æŅŃÖŖ”÷ABC£¬AB£½AC£¬DĪŖBCÉĻŅ»µć£¬EĪŖACÉĻŅ»µć£¬AD£½AE£®
£Ø1£©Čē¹ū”ĻBAD£½10”ć£¬”ĻDAE£½30”ć£¬ÄĒĆ“”ĻEDC£½”” ”””ć£®
£Ø2£©Čē¹ū”ĻABC£½60”ć£¬”ĻADE£½70”ć£¬ÄĒĆ“”ĻBAD£½”” ”””ć£¬”ĻCDE£½”” ”””ć£®
£Ø3£©Éč”ĻBAD£½¦Į£¬”ĻCDE£½¦Ā²ĀĻė¦Į£¬¦ĀÖ®¼äµÄ¹ŲĻµŹ½£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÕż±ČĄżŗÆŹży=kx¾¹żµćA£¬µćAŌŚµŚĖÄĻóĻŽ£¬¹żµćA×÷AH”ĶxÖį£¬“¹×ćĪŖµćH£¬µćAµÄŗį×ų±źĪŖ3£¬ĒŅ”÷AOHµÄĆ껿ĪŖ3£®
£Ø1£©ĒóÕż±ČĄżŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ŌŚxÖįÉĻÄÜ·ńÕŅµ½Ņ»µćP£¬Ź¹”÷AOPµÄĆ껿ĪŖ5£æČō“ęŌŚ£¬ĒóµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³Äź5ŌĀ£¬ĪŅ¹śÄĻ·½Ä³Ź”A”¢BĮ½ŹŠŌāŹÜŃĻÖŲŗéĄŌŌÖŗ¦£¬1.5ĶņČĖ±»ĘČ×ŖŅĘ£¬ĮŚ½üĻŲŹŠC”¢D»ńÖŖA”¢BĮ½ŹŠ·Ö±š¼±Šč¾ČŌÖĪļ׏200¶ÖŗĶ300¶ÖµÄĻūĻ¢ŗ󣬾ö¶Øµ÷ŌĖĪļ׏֧Ō®ŌÖĒų£®ŅŃÖŖCŹŠÓŠ¾ČŌÖĪļ׏240¶Ö£¬DŹŠÓŠ¾ČŌÖĪļ׏260¶Ö£¬ĻÖ½«ÕāŠ©¾ČŌÖĪļ׏ȫ²æµ÷ĶłA”¢BĮ½ŹŠ£®ŅŃÖŖ“ÓCŹŠŌĖĶłA”¢BĮ½ŹŠµÄ·ŃÓĆ·Ö±šĪŖĆæ¶Ö20ŌŖŗĶ25ŌŖ£¬“ÓDŹŠŌĖĶłĶłA”¢BĮ½ŹŠµÄ·ŃÓƱšĪŖĆæ¶Ö15ŌŖŗĶ30ŌŖ£¬Éč“ÓDŹŠŌĖĶłBŹŠµÄ¾ČŌÖĪļ׏ĪŖx¶Ö£®
£Ø1£©ĒėĢīŠ“ĻĀ±ķ
A£Ø¶Ö£© | B£Ø¶Ö£© | ŗĻ¼Ę£Ø¶Ö£© | |
C | ”” ”” | ”” ”” | 240 |
D | ”” ”” | x | 260 |
×Ü¼Ę£Ø¶Ö£© | 200 | 300 | 500 |
£Ø2£©ÉčC”¢DĮ½ŹŠµÄ×ÜŌĖ·ŃĪŖwŌŖ£¬ĒówÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£»
£Ø3£©¾¹żĒĄŠŽ£¬“ÓDŹŠµ½BŹŠµÄĀ·æöµĆµ½ĮĖøÄÉĘ£¬Ėõ¶ĢĮĖŌĖŹäŹ±¼ä£¬ŌĖ·ŃĆæ¶Ö¼õÉŁmŌŖ£Øm£¾0£©£¬ĘäÓąĀ·ĻßŌĖ·Ń²»±ä£®ČōC”¢DĮ½ŹŠµÄ×ÜŌĖ·ŃµÄ×īŠ”Öµ²»Š”ÓŚ10320ŌŖ£¬ĒómµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ6”Į6µÄ·½øńÖ½ÖŠ£¬ĆæøöŠ”·½øń¶¼ŹĒ±ß³¤ĪŖ1µÄÕż·½ŠĪ£¬ĘäÖŠA”¢B”¢CĪŖøńµć£¬×÷”÷ABCµÄĶā½ÓŌ²”ŃO£¬Ōņ»”ACµÄ³¤µČÓŚ£Ø””””£©
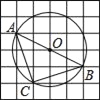
A. ¦Š B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬EŹĒADµÄÖŠµć£¬ŃÓ³¤CE£¬BA½»ÓŚµćF£¬Į¬½ÓAC£¬DF£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪACDFŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©µ±CFĘ½·Ö”ĻBCDŹ±£¬Š“³öBCÓėCDµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży=kx+bµÄĶ¼ĻólÓė×ų±źÖį·Ö±š½»ÓŚµćE£¬F£¬ÓėĖ«ĒśĻßy=©![]() £Øx£¼0£©½»ÓŚµćP£Ø©1£¬n£©£¬ĒŅFŹĒPEµÄÖŠµć£¬Ö±Ļßx=aÓėl½»ÓŚµćA£¬ÓėĖ«ĒśĻß½»ÓŚµćB£Ø²»Ķ¬ÓŚA£©£¬PA=PB£¬Ōņa=________£®
£Øx£¼0£©½»ÓŚµćP£Ø©1£¬n£©£¬ĒŅFŹĒPEµÄÖŠµć£¬Ö±Ļßx=aÓėl½»ÓŚµćA£¬ÓėĖ«ĒśĻß½»ÓŚµćB£Ø²»Ķ¬ÓŚA£©£¬PA=PB£¬Ōņa=________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē¹ūŅ»ŌŖ¶ž“Ī·½³Ģax2£«bx£«c£½0(a”Ł0)Āś×ć4a£2b£«c£½0£¬ĒŅÓŠĮ½øöĻąµČµÄŹµŹżøł£¬Ōņ( )
A. b£½aB. c£½2aC. a(x£«2)2£½0(a”Ł0)D. a(x£2)2£½0(a”Ł0)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĆę½ā·½³Ģ![]() µÄ²½Öč£¬ŌŚŗóĆęµÄŗįĻßÉĻĢīŠ““Ė²½ÖčµÄŅĄ¾Ż£ŗ
µÄ²½Öč£¬ŌŚŗóĆęµÄŗįĻßÉĻĢīŠ““Ė²½ÖčµÄŅĄ¾Ż£ŗ
½ā£ŗČ„·ÖÄø£¬µĆ![]() .¢ŁŅĄ¾Ż£ŗ_________
.¢ŁŅĄ¾Ż£ŗ_________
Č„ĄØŗÅ£¬µĆ![]() .
.
ŅĘĻī£¬µĆ![]() .¢ŚŅĄ¾Ż£ŗ__________
.¢ŚŅĄ¾Ż£ŗ__________
ŗĻ²¢Ķ¬ĄąĻī£¬µĆ![]() .
.
ĻµŹż»ÆĪŖ1£¬µĆ![]() .
.
”ą![]() ŹĒŌ·½³ĢµÄ½ā.
ŹĒŌ·½³ĢµÄ½ā.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com