
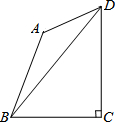
 如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.
如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.分析 (1)先根据锐角三角函数的定义求出CD的长,再根据勾股定理即可得出结论;
(2)过点D作DE⊥AB交BA延长线于点E,先判断出△ADE的形状,再根据勾股定理即可得出结论.
解答 解: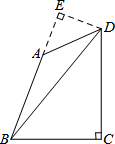 (1)在Rt△BCD中,∠BCD=90°,BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$,
(1)在Rt△BCD中,∠BCD=90°,BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$,
∴$\frac{4}{CD}$=$\frac{\sqrt{6}}{3}$.
∴CD=2$\sqrt{6}$,
∴由勾股定理得BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=2$\sqrt{10}$;
(2)如图,过点D作DE⊥AB交BA延长线于点E.
∵∠BAD=135°,
∴∠EAD=∠ADE=45°.
∴AE=ED.
设AE=ED=x,则AD=$\sqrt{2}$x.
∵DE2+BE2=BD2,
∴x2+(x+4)2=(2$\sqrt{10}$)2.
解得x1=-6舍),x2=2
∴AD=$\sqrt{2}$x=2$\sqrt{2}$
点评 本题考查的是勾股定理及锐角三角函数的定义,熟知锐角三角函数的定义是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
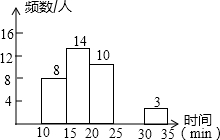 某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.| 时间分段/min | 频(人)数 | 百分比 |
| 10≤x<15 | 8 | 20% |
| 15≤x<20 | 14 | a |
| 20≤x<25 | 10 | 25% |
| 25≤x<30 | b | 12.50% |
| 30≤x<35 | 3 | 7.50% |
| 合计 | c | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
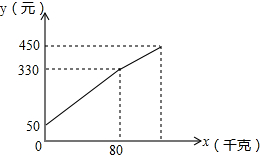 李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
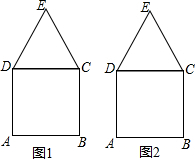 如图,已知正方形ABCD和等边三角形CDE,请按要求完成下列画图,要求:①仅用无刻度的直尺,②保留必要的画图痕迹.
如图,已知正方形ABCD和等边三角形CDE,请按要求完成下列画图,要求:①仅用无刻度的直尺,②保留必要的画图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com