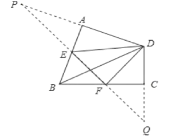
【题目】如图，在四边形ABCD中，∠A=∠C=90°，∠B=α，在AB，BC上分别找一点E,F,使△DEF的周长最小，此时，∠EDF=______。（用含α的代数式表示）
【答案】180°2α
【解析】
根据要使△DEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出D关于AB和BC的对称点P,Q,结合四边形的内角和即可得出答案。
如图，作点D关于BA的对称点P，点D关于BC的对称点Q，连接PQ，交AB于E，交BC于F，则点E，F即为所求。
∵四边形ABCD中,∠A=∠C=90°，∠B=α，
∴∠PDQ=180°α，
在三角形PDQ中，∠P+∠Q=180°-∠PDQ =α，
∵点P与点D关于AB对称，点D与点Q关于DQ对称，
∴∠P=∠ADE，∠Q=∠FDQ
∴∠ADE+ FDQ=∠P+∠Q=α
∴∠EDF=∠PDQ-（∠ADE+ ∠FDQ）=180°2α
科目：初中数学 来源： 题型：
【题目】为了参加学校举行的传统文化知识竞赛，某班进行了四次模拟训练，将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图：
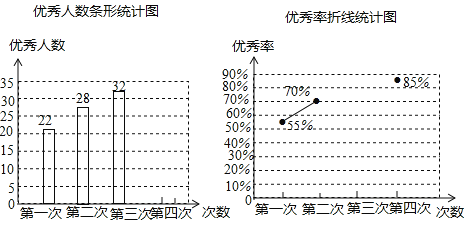
（1）求该班总人数；
（2）根据计算，请你补全两个统计图；
（3）已知该班甲同学四次训练成绩为85，95，85，95，乙同学四次成绩分别为85，90，95，90，现需从甲、乙两同学中选派一名同学参加校级比赛，你认为应该选派哪位同学并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在△ABC中，AB=AC，D是BC的中点，点E在AD上.
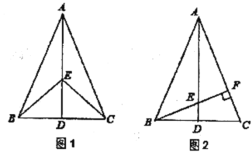
（1）求证：BE=CE；
（2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其他条件不变.求证：EF=CF.
查看答案和解析>>
科目：初中数学 来源： 题型：
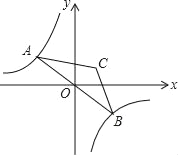
【题目】如图，点A是双曲线y=﹣
在第二象限分支上的一个动点，连接AO并延长交另一分支于点B，以AB为底作等腰△ABC，且∠ACB=120°，点C在第一象限，随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y=
上运动，则k的值为（ ）
A. 3 B. 4 C. 2.5 D. 7
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABE中，∠BAE＝105°，AE的垂直平分线MN交BE于点C，且AB＝CE，则∠B的度数是( )
A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目：初中数学 来源： 题型：
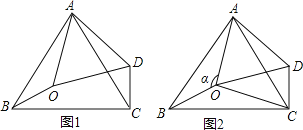
【题目】如图1，在△ABC中，∠BAC=60°，点0是△ABC内一点，△AB0
△ACD，连接OD.
（1）求证△AOD为等边三角形。
（2）如图2，连接OC，若∠BOC=130°，∠AOB=
.
①求∠OCD的度数
②当△OCD是等腰三角形时，求∠的度数
、
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，已知点A（﹣3，3），B（﹣5，1），C（﹣2，0），P（a，b）是△ABC的边AC上任意一点，△ABC经过平移后得到△A1B1C1，点P的对应点为P1（a+6，b﹣2）．
（1）平移后的三个顶点坐标分别为：.A1（ ），B1（ ），C1（ ）.
（2）在上图中画出平移后三角形A1B1C1；
（3）画出△AOA1并求出△AOA1的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法中：
两条直线相交只有一个交点；
两条直线不是一定有公共点；
直线
与直线
是两条不同的直线；
两条不同的直线不能有两个或更多公共交点．
其中正确的是（ ）
A. （1）（2） B. （1）（4） C. （1）（2）（4） D. （2）（3）（4）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com