
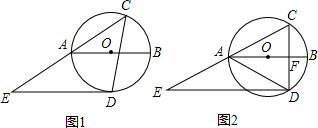
分析 (1)如图1中,连接OD,欲证明ED是切线,只要证明∠EDO=90°即可.
(2)如图2中,连接BC,利用勾股定理.以及直角三角形30度性质求出CD、DE即可.
解答 (1)证明:如图1中,连接OD.
∵∠C=45°,
∴∠AOD=2∠C=90°,
∵ED∥AB,
∴∠AOD+∠EDO=180°,
∴∠EDO=90°,
∴ED⊥OD,
∴ED是⊙O切线.
(2)解:如图2中,连接BC,
∵CF=DF,
∴AF⊥CD,
∴AC=AD,
∴∠ACD=∠ADC,
∵AB∥ED,
∴ED⊥DC,
∴∠EDC=90°,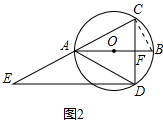
在RT△ACB中,∵∠ACB=90°,∠CAB=30°,AB=2,
∴BC=1,AC=$\sqrt{3}$,
∴CF=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$,CD=2CF=$\sqrt{3}$,
在RT△ECD中,
∵∠EDC=90°,CD=$\sqrt{3}$,∠E=∠CAB=30°,
∴EC=2CD=2$\sqrt{3}$,ED=$\sqrt{E{C}^{2}-C{D}^{2}}$=3,
∴S△ECD=$\frac{1}{2}$•ED•CD=$\frac{3\sqrt{3}}{2}$.
点评 本题考查切线的性质和判定、圆的有关知识、勾股定理等知识,解题的关键是灵活运用这些知识,属于基础题,中考常考题型.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
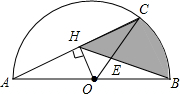 如图,AB为半圆的直径,弧AC为弧CB的两倍,OH⊥AC于点H,BH与OC交于E,己知AC=2$\sqrt{3}$.
如图,AB为半圆的直径,弧AC为弧CB的两倍,OH⊥AC于点H,BH与OC交于E,己知AC=2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二七纪念塔是我省郑州市的标志性建筑,某兴趣小组为了测量二七纪念塔的高度,进行了如下的研究.如图,AB为二七纪念塔,从地面C点看塔顶A点,仰角为45°,到建筑DE顶端E点后,从E点看塔顶A点,仰角为60°,C、D、B三点在同一直线上.已知建筑DE高度为35.3米,∠ECD=37°,求二七纪念塔AB的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;$\sqrt{3}$≈1.732)
二七纪念塔是我省郑州市的标志性建筑,某兴趣小组为了测量二七纪念塔的高度,进行了如下的研究.如图,AB为二七纪念塔,从地面C点看塔顶A点,仰角为45°,到建筑DE顶端E点后,从E点看塔顶A点,仰角为60°,C、D、B三点在同一直线上.已知建筑DE高度为35.3米,∠ECD=37°,求二七纪念塔AB的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com