
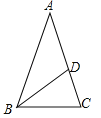
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断![]() 与ACCD的大小关系;
与ACCD的大小关系;
(2)求∠ABD的度数.
【答案】(1)![]() ;(2)36°.
;(2)36°.
【解析】
试题分析:(1)先求得AD、CD的长,然后再计算出![]() 与ACCD的值,从而可得到
与ACCD的值,从而可得到![]() 与ACCD的关系;
与ACCD的关系;
(2)由(1)可得到![]() =ACCD,然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数.
=ACCD,然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数.
试题解析:(1)∵AD=BC=![]() ,∴
,∴![]() =
=![]() =
=![]() .
.
∵AC=1,∴CD=![]() =
=![]() ,∴
,∴![]() ;
;
(2)∵![]() ,∴
,∴![]() ,即
,即![]() ,又∵∠C=∠C,∴△ABC∽△BDC,∴
,又∵∠C=∠C,∴△ABC∽△BDC,∴![]() ,又∵AB=AC,∴BD=BC=AD,∴∠A=∠ABD,∠ABC=∠C=∠BDC.
,又∵AB=AC,∴BD=BC=AD,∴∠A=∠ABD,∠ABC=∠C=∠BDC.
设∠A=∠ABD=x,则∠BDC=∠A+∠ABD=2x,∴∠ABC=∠C=∠BDC=2x,∴∠A+∠ABC+∠C=x+2x+2x=180°,解得:x=36°,∴∠ABD=36°.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】比较下列四个算式结果的大小(在横线上填“>”“<”或“=”).
(1)42+52_______2×4×5;
(2)(-1)2+22_______2×(-1)×2;
(3)(-3)2+![]() 2______2×(-3)×
2______2×(-3)×![]() ;
;
(4)32+32_______2×3×3;
(5)请通过观察归纳,写出反映这种规律的一般结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
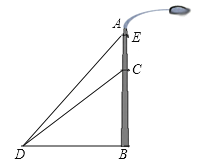
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“数学晚会”上,七年级的10个同学藏在10个大盾牌后面,男同学盾牌前面的结果是一
个正数,女同学盾牌前面的结果是一个负数,这10个盾牌如图所示,请你通过计算,求出盾牌后面男、女同学各有多少人.
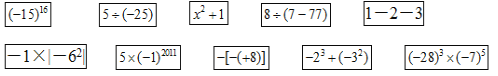
查看答案和解析>>
科目:初中数学 来源: 题型:
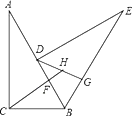
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,下列说法正确的是( )
A.两直线的位置关系是平行、垂直和相交
B.不平行的两条直线一定互相垂直
C.不垂直的两条直线一定互相平行
D.不相交的两条直线一定互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数:2,1,3,x,7,﹣9,…,满足“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b”,例如这组数中的第三个数“3”是由“2×2﹣1”得到的,那么这组数中x表示的数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.有一组对边平行的四边形是平行四边形B.对角线互相垂直的四边形是菱形
C.有一组邻边相等的平行四边形是菱形D.对角线互相垂直平分的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com