
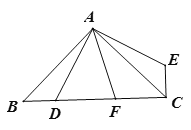
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.
【答案】(1)证明见解析;(2)BD2+FC2=DF2,理由见解析;(3)![]() .
.
【解析】
(1)根据垂直的定义以及直角,得到∠BAD=∠CAE,然后SAS证明即可;
(2)根据等腰直角三角形的性质得到∠B=∠ACB=45°,然后由(1)的结论得到∠ACE=45°,BD=CE,从而得到∠FCE=90°,根据勾股定理得出![]() ,再根据SAS证明△DAF≌△EAF,根据全等三角形的性质得到DF=FE,从而得到结论;
,再根据SAS证明△DAF≌△EAF,根据全等三角形的性质得到DF=FE,从而得到结论;
(3)过点A作![]() 于G,根据(2)的结论得到DF=5,然后根据等腰直角三角形的性质求出DG,最后根据勾股定理求解即可.
于G,根据(2)的结论得到DF=5,然后根据等腰直角三角形的性质求出DG,最后根据勾股定理求解即可.
(1)∵![]()
∴![]()
又∵![]()

∴![]()
在△ABD和△ACE中

∴△ABD≌△ACE;
(2)![]() 理由如下:
理由如下:
连接FE, ∵![]()
∴![]()
由(1)知△ABD≌△ACE
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵AF平分![]()
∴![]()
在△DAF和△EAF中

∴△DAF≌△EAF
∴![]() .
.
∴![]() ;
;
(3)过点A作![]() 于G
于G
由(2)知![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴在![]() 中
中![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.
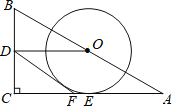
(1)判断直线DF与⊙O的位置关系,并说明理由;
(2)当∠A=30°,CF![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江苏省常州市)为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:

根据统计图所提供的信息,解答下列问题:
(1)本次抽样调查中的样本容量是 ;
(2)补全条形统计图;
(3)该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
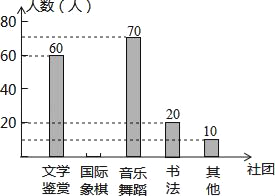
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
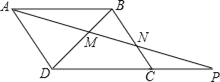
【题目】如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)图中相似三角形共有_____对;
(2)证明:AM2=MNMP;
(3)若AD=6,DC:CP=2:1,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
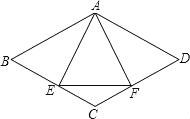
【题目】已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;
(1)求证:△ABE≌△ADF.
(2)若菱形ABCD中,AB=4,∠C=120°,∠EAF=60°,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )
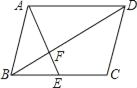
A. BF=![]() DFB. S△AFD=2S△EFBC. 四边形AECD是等腰梯形D. ∠AEB=∠ADC
DFB. S△AFD=2S△EFBC. 四边形AECD是等腰梯形D. ∠AEB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
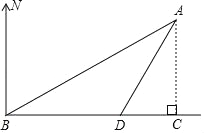
【题目】如图,海中有一小岛A,它周围8海里内有暗礁,渔船由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.
(1)求∠BAD的度数;
(2)如果渔船不改变航线继续向东航行,有没有触礁的危险?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com