
【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G. 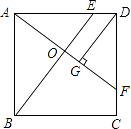
(1)求证:AF⊥BE;
(2)试探究线段AO、BO、GO的长度之间的数量关系;
(3)若GO:CF=4:5,试确定E点的位置.
【答案】
(1)证明:∵ABCD为正方形,且DE=CF,
∴AE=DF,AB=AD,∠BAE=∠ADF=90°,
在△ABE和△DAF,
∵  ,
,
∴△ABE≌△DAF,
∴∠ABE=∠DAF,又∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AOE=90°,即AF⊥BE
(2)解:BO=AO+OG.
理由:由(1)的结论可知,
∠ABE=∠DAF,∠AOB=∠DGA=90°,AB=AD,
在△ABO和△DAG中,
∵ 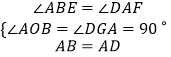 ,
,
则△ABO≌△DAG,
所以,BO=AG=AO+OG
(3)解:过E点作EH⊥DG,垂足为H,
由矩形的性质,得EH=OG,
∵DE=CF,GO:CF=4:5,∴EH:ED=4:5,
∵AF⊥BE,AF⊥DG,∴OE∥DG,
∴∠AEB=∠EDH,△ABE∽△HED,
∴AB:BE=EH:ED=4:5,
在Rt△ABE中,AE:AB=3:4,
故AE:AD=3:4,
即AE= ![]() AD.
AD.
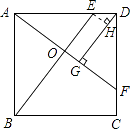
【解析】(1)由DE=CF及正方形的性质,得出AE=DF,AB=AD,∠BAE=∠ADF=90°,证明△ABE≌△DAF,得出∠ABE=∠DAF,而∠ABE+∠AEB=90°,利用互余关系得出∠AOE=90°即可;(2)由(1)的结论可证△ABO≌△DAG,得BO=AG=AO+OG;(3)过E点作EH⊥DG,垂足为H,则EH=OG,由DE=CF,GO:CF=4:5,得EH:ED=4:5,而AF⊥BE,AF⊥DG,则OE∥DG,∠AEB=∠EDH,△ABE∽△HED,利用相似比得出AB:BE,由勾股定理得出AE:AB,从而得出AE:AD.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
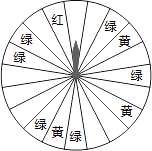
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°. 
(1)求∠APB的大小;
(2)若PO=20cm,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有以下说法:其中正确的说法有( )
(1)开方开不尽的数是无理数;
(2)无理数是无限循环小数
(3)无理数包括正无理数和负无理数;
(4)无理数都可以用数轴上的点来表示;
(5)循环小数都是有理数
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q. 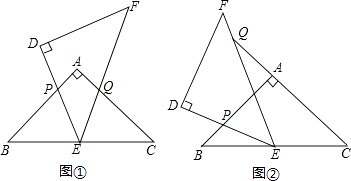
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ= ![]() 时,P、Q两点间的距离 (用含a的代数式表示).
时,P、Q两点间的距离 (用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
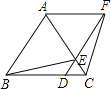
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;
(2)判断四边形ABDF是怎样的四边形,并说明理由;
(3)若AB=6,BD=2DC,求四边形ABEF的面积..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com