
| A. | $\frac{4}{5}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
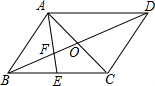 已知:如图,四边形ABCD中,AC与BD交于点O,且OA=OC,AD∥BC
已知:如图,四边形ABCD中,AC与BD交于点O,且OA=OC,AD∥BC查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差越大,说明数据就越稳定 | |
| B. | “预计本题的正确率是95%”表示100位考生中一定有95人做对 | |
| C. | 两边及其一边的对角对应相等的两个三角形一定全等 | |
| D. | 圆内接四边形对角互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
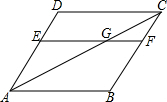 如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )
如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
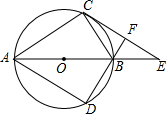 如图,四边形ACBD是⊙O的内接四边形,AB为直径,过C作⊙O的切线交AB的延长于E,DB⊥CE,垂足为F.
如图,四边形ACBD是⊙O的内接四边形,AB为直径,过C作⊙O的切线交AB的延长于E,DB⊥CE,垂足为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com