
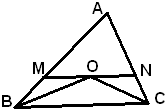
 14、如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )
14、如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )科目:初中数学 来源: 题型:
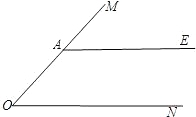 如图,A是∠MON边OM上一点,AE∥ON.
如图,A是∠MON边OM上一点,AE∥ON.查看答案和解析>>
科目:初中数学 来源: 题型:
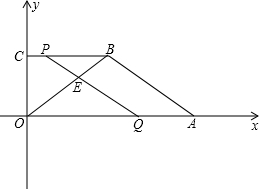 2个单位/秒的速度向点O 移动.设点P、Q同时出发,运动的时间为t(秒)
2个单位/秒的速度向点O 移动.设点P、Q同时出发,运动的时间为t(秒)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC,∠ABC=90°,CO平分∠ACB交于AB于O,D为AC上一点,且CD=CB,E为AO上一点,OE=OB,连接DE
如图,在Rt△ABC,∠ABC=90°,CO平分∠ACB交于AB于O,D为AC上一点,且CD=CB,E为AO上一点,OE=OB,连接DE查看答案和解析>>
科目:初中数学 来源:百分学生作业本课时3练1测 七年级数学(下) 适用人教课标版学生 人教课标版 题型:059
试试你的观察能力和分析能力.
如图,已知CB∥OA,∠C=100°,E、F分别为CB上的点,且OB平分∠FOA,OE平分∠COF.
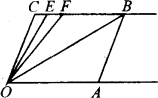
(1)求∠EOB的度数;
(2)若左、右移动AB,那么∠EOB的值是否随之发生变化?若变,找出变化规律;若不变,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com