
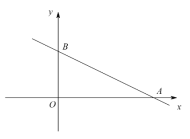
【题目】已知:如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 和点
和点![]() ,并与
,并与![]() 轴相交于另一点
轴相交于另一点![]() ,对称轴与
,对称轴与![]() 轴相交于点
轴相交于点![]() .
.
(1)求抛物线的表达式;
(2)求证:![]() ;
;
(3)如果点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)见解析;(3)P(
;(2)见解析;(3)P(![]() ,
,![]() )
)
【解析】
(1)利用一次函数,先用含有b的式子表示出A、B两点的坐标,然后代入二次函数可求得b和a的值;
(2)利用两个三角形夹角相等,且夹边成比例证明;
(3)先利用△BCP∽△BAC得到BP的长,再利用△BOA∽△BHP得到点P的横坐标,同理得到纵坐标.
(1)∵一次函数为![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]()
∴A(-2b,0),B(0,-b)
将点B代入抛物线![]() 得:-b=4,解得:b=-4
得:-b=4,解得:b=-4
∴A(8,0),B(0,4)
将点A代入抛物线![]() 得:0=64a-32a+4,解得:a=
得:0=64a-32a+4,解得:a=![]()
∴抛物线解析式为:![]()
(2)∵抛物线为![]()
∴对称轴为:x=![]()
∴D(2,0),图形如下:

根据坐标关系得:OD=2,OA=8,OB=4
∵∠BOD=∠BOA
又∵![]()
∴![]()
(3)图形如下,连接CP:
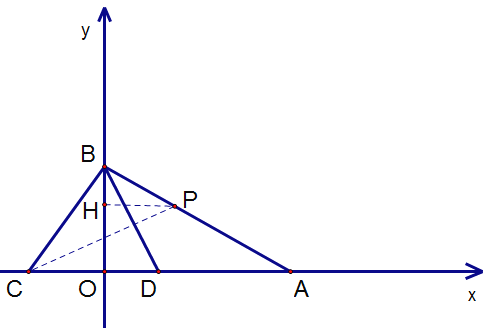
∵△BOD∽△AOB
设∠OBD=∠BAO=a,则∠BCP=∠DBO=a
∴∠BCP=∠BAO=a
∵∠CBP=∠CBA
∴△BCP∽△BAC
∴![]()
∵B(0,4),C(-4,0),A(8,0)
∴根据勾股定理:BC=4![]() ,AB=4
,AB=4![]()
∴BP=![]()
过点P作x轴的平行线交y轴于点H
∵PH∥x轴
∴![]() ,解得:PH=
,解得:PH=![]() ,即点P的横坐标为
,即点P的横坐标为![]()
同理可得点P的纵坐标为![]()
∴P(![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
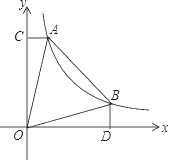
【题目】如图,A、B两点在反比例函数![]() (k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(1)若△AOC的面积为4,求k值;
(2)若a=1,b=k,当AO=AB时,试说明△AOB是等边三角形;
(3)若OA=OB,证明:OC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园生活,展现同学们英语表达的风采,某校组织了“英语风采大赛”,大赛共设置四个比赛项目.八年级六班的同学们踊跃报名,在“才艺表演”项目中,小怡报名表演古筝,小宏报名表演小提琴,小童报名表演笛子,小灿和小源报名唱英文歌曲.为了取得良好的节目效果,体现公平公正.文体委员决定采用以下方法搭配组合节目:制作5张完全相同的卡片,正面分别写上报名参加比赛同学的姓名,将卡片反面朝上洗匀,然后随机抽取卡片,卡片正面是谁的名字,谁就代表班级参加比赛.
(1)随机抽取一张卡片,求六班才艺表演项目是“乐器独奏”的概率;
(2)随机抽取两张卡片,请用树状图或列表法求小宏和小灿组合参加比赛的概率.(注:可以用![]() 分别表示小怡,小宏,小童,小灿,小源的名字)
分别表示小怡,小宏,小童,小灿,小源的名字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),并与![]() 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
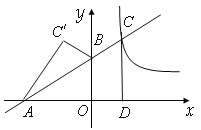
(1)求一次函数与反比例函数的解析式;
(2)若点C'是点C关于y轴的对称点,请求出△ABC'的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=AB,点F为CE的中点,点G在线段CD上,联结DF,交AG于点M,交EG于点N,且∠DFC=∠EGC.
(1)求证:CG=DG;
(2)求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com