
【题目】如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)求证:四边形ACPB是平行四边形;
(2)求直线BE的解析式及点P的坐标.

【答案】(1)详见解析;(2)点P的坐标为(9,3).
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A、C的坐标,进而可得出∠CAO=45°,结合∠PCA=135°可得出∠CAO+∠PCA=180°,利用“同旁内角互补,两直线平行”可得出AB∥CP,同理可求出∠ABE=45°=∠CAO,利用“内错角相等,两直线平行”可得出AC∥BP,再利用平行四边形的判定定理可证出四边形ACPB为平行四边形;
(2)由点B、E的坐标,利用待定系数法可求出直线BE的解析式,由AB∥CP可得出点P的纵坐标,再利用一次函数图象上点的坐标特征即可求出点P的坐标.
(1)∵直线y=x+3与x轴、y轴分别相交于A、C两点,
∴点A的坐标为(﹣3,0),点C的坐标为(0,3),
∴OA=OC.
∵∠AOC=90°,
∴∠CAO=45°.
∵∠PCA=135°,
∴∠CAO+∠PCA=180°,
∴AB∥CP.
∵点B的坐标为(6,0),点E的坐标为(0,﹣6),
∴OB=OE.
∵∠BOE=90°,
∴∠OBE=45°,
∴∠CAO=∠ABE=45°,
∴AC∥BP,
∴四边形ACPB为平行四边形.
(2)设直线BE的解析式为y=kx+b(k≠0),
将B(6,0)、E(0,﹣6)代入y=kx+b,得:
![]() ,解得:
,解得: ![]()
∴直线BE的解析式为y=x﹣6.
∵AB∥CP,
∴点P的纵坐标是3,
∴点P的坐标为(9,3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】等腰三角形一腰上的高与另一腰的夹角为 45°,则这个等腰三角形的底角为( )
A.67°B.67.5°C.22.5°D.67.5°或 22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大爷饭后出去散步,从家中走20分钟到离家900米的公园,与朋友聊天10分钟后,用15分钟返回家中.下面图形表示王大爷离时间x(分)与离家距离y(米)之间的关系是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )

A.(4,2) B.(6,0) C.(6,3) D.(6,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个长方形锥被分割成若干个大小不同的正方,则说这个长方形是完美长方形,如图,有一个完美长方形被分成![]() 个大小不同的正方形,其中最小正方形(阴影部分)的边长是
个大小不同的正方形,其中最小正方形(阴影部分)的边长是![]() ,设正方形①的边长为
,设正方形①的边长为![]() ,请直接用含有
,请直接用含有![]() 的代数式表示出正方形②③④⑤的边长.
的代数式表示出正方形②③④⑤的边长.

②:__________③:__________④:__________⑤:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() ,请回答问题:
,请回答问题:
(![]() )请直接写出
)请直接写出![]() 、
、![]() 、
、![]() 的值,
的值,![]() ______,
______,![]() ____,
____,![]() ______.
______.
(![]() )数轴上
)数轴上![]() 、
、![]() 、
、![]() 三个数所对应的分别为
三个数所对应的分别为![]() 、
、![]() 、
、![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 、
、![]() 、
、![]() 同时开始在数轴上运动,若点
同时开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,点
个单位长度的速度向左运动,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动.
个单位长度的速度向右运动.
①经过![]() 秒后,求出点
秒后,求出点![]() 与点
与点![]() 之间的距离
之间的距离![]() .
.
②经过![]() 秒后,请问:
秒后,请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理上;若不变,请求其值.
的变化而改变?若变化,请说明理上;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年来全国各省市市政府民生实事之一的公共自行车建设工作已基本完成,网上资料显示呼和浩特市某部门对14年4月份中的7天进行了公共自行车日租车辆的统计,结果如图:
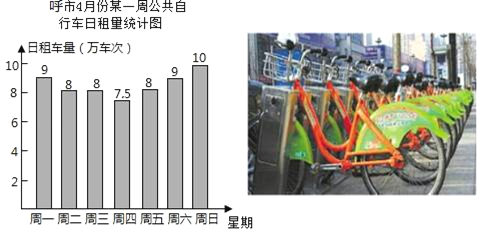
(1)求这7天日租车量的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)该市共租车多少万车次;
(3)资料显示,呼市政府在公共自行车建设项目中共投入9600万元,估计2014年共租车3200万车次,每车次平均收入租车费0.1元,求2014年该市租车费收入占总投入的百分率(精确到0.1%).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2018处,则点A2018与点A0间的距离是( )

A. 0 B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com