
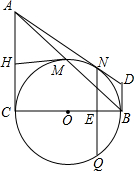
 如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.
如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.分析 (1)连接OH、OM,易证OH是△ABC的中位线,利用中位线的性质可证明△COH≌△MOH,所以∠HCO=∠HMO=90°,从而可知MH是⊙O的切线;
(2)由切线长定理可知:MH=HC,再由点M是AC的中点可知AC=3,由tan∠ABC=$\frac{3}{4}$,所以BC=4,从而可知⊙O的半径为2;
(3)连接CN,AO,CN与AO相交于I,由AC、AN是⊙O的切线可知AO⊥CN,利用等面积可求出可求得CI的长度,设CE为x,然后利用勾股定理可求得CE的长度,利用垂径定理即可求得NQ.
解答 解:(1)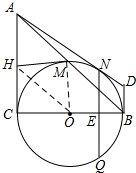 连接OH、OM,
连接OH、OM,
∵H是AC的中点,O是BC的中点,
∴OH是△ABC的中位线,
∴OH∥AB,
∴∠COH=∠ABC,∠MOH=∠OMB,
又∵OB=OM,
∴∠OMB=∠MBO,
∴∠COH=∠MOH,
在△COH与△MOH中,
$\left\{\begin{array}{l}{OC=OM}\\{∠COH=∠MOH}\\{OH=OH}\end{array}\right.$,
∴△COH≌△MOH(SAS),
∴∠HCO=∠HMO=90°,
∴MH是⊙O的切线;
(2)∵MH、AC是⊙O的切线,
∴HC=MH=$\frac{3}{2}$,
∴AC=2HC=3,
∵tan∠ABC=$\frac{3}{4}$,
∴$\frac{AC}{BC}$=$\frac{3}{4}$,
∴BC=4,
∴⊙O的半径为2;
(3)连接OA、CN、ON,OA与CN相交于点I,
∵AC与AN都是⊙O的切线,
∴AC=AN,AO平分∠CAD,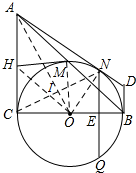
∴AO⊥CN,
∵AC=3,OC=2,
∴由勾股定理可求得:AO=$\sqrt{13}$,
∵$\frac{1}{2}$AC•OC=$\frac{1}{2}$AO•CI,
∴CI=$\frac{6\sqrt{13}}{13}$,
∴由垂径定理可求得:CN=$\frac{12\sqrt{13}}{13}$,
设OE=x,
由勾股定理可得:CN2-CE2=ON2-OE2,
∴$\frac{144}{13}$-(2+x)2=4-x2,
∴x=$\frac{10}{13}$,
∴OE=$\frac{10}{13}$,
由勾股定理可求得:EN=$\frac{24}{13}$,
∴由垂径定理可知:NQ=2EN=$\frac{48}{13}$.
点评 本题考查圆的综合问题,涉及垂径定理,勾股定理,全等三角形的判定与性质,切线的判定等知识内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.


科目:初中数学 来源: 题型:选择题
| A. | 505 | B. | 510 | C. | 520 | D. | 550 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,4) | B. | (-1,-8) | C. | (-2,-4) | D. | (4,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)
如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
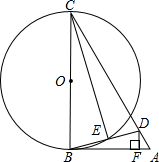 如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
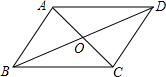 如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )| A. | AB=AD | B. | AC⊥BD | C. | AC=BD | D. | ∠BAC=∠DAC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com