
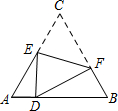
 如图,D是等边△ABC边AB上的一点,且AD:DB=1:3,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=5:7.
如图,D是等边△ABC边AB上的一点,且AD:DB=1:3,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=5:7. 分析 借助翻折变换的性质得到DE=CE、CF=DF;设AD=k,则DB=3k;根据相似三角形的判定与性质即可解决问题.
解答 解:设AD=k,则DB=3k,
∵△ABC为等边三角形,
∴AB=AC=4k,∠A=∠B=∠C=∠EDF=60°,
∴∠EDA+∠FDB=120°,
又∵∠EDA+∠AED=120°,
∴∠FDB=∠AED,
∴△AED∽△BDF,
由折叠,得CE=DE,CF=DF
∴△AED的周长为5k,△BDF的周长为7k,
∴△AED与△BDF的相似比为5:7
∴CE:CF=DE:DF=5:7.
故答案为5:7.
点评 主要考查了翻折变换的性质及其应用问题、相似三角形的判定和性质,解题的关键是利用相似三角形的周长之比等于相似比,学会根据条件设相应的线段(用字母a表示),对综合的分析问题解决问题的能力提出了较高的要求.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
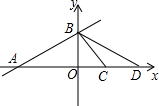 已知一次函数y=$\frac{{\sqrt{2}}}{3}$x+$\sqrt{2}$的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD和∠ABD是两个不相等的钝角,求经过B、D两点的一次函数的解析式.
已知一次函数y=$\frac{{\sqrt{2}}}{3}$x+$\sqrt{2}$的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD和∠ABD是两个不相等的钝角,求经过B、D两点的一次函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
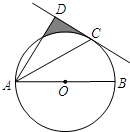 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.若AB=$2\sqrt{6}$,∠BAC=30°,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}$-π.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.若AB=$2\sqrt{6}$,∠BAC=30°,则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}$-π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com