

分析 (1)根据良的人数和所占的百分比即可求出m的值;
(2)用总人数减去优、良、差的人数,求出中的人数,用优的人数除以总人数,即可求出优所占的百分比,从而补全统计图;
(3)用360°乘以等级为“中”的所占的百分比,即可求出圆心角的度数;
(4)用全区九年级的人数乘以优所占的百分比即可得出答案.
解答 解:(1)根据题意得:m=$\frac{44}{44%}$=100(人);
(2)成绩为中的人数是:100-20-44-16=20(人),
优所占的百分比是:$\frac{20}{100}$×100%=20%;
补图如下: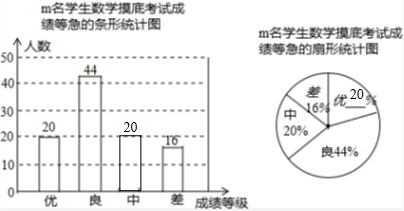
(3)成绩等级为“中”的扇形所对应的圆心角的度数是:360×20%=72°;
(4)根据题意得:
1180×20%=236(人),
答:这次考试数学成绩等级为“优”的人数有236人.
点评 本题考查的是条形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.用到的知识点为:总体数目=部分数目÷相应百分比.概率=所求情况数与总情况数之比.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
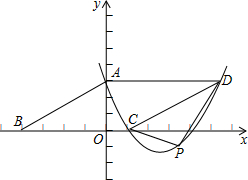 如图所示,在平面直角坐标系中,△ABC的顶点坐标分别为点A(0,3)、B(-4,0)、C(1,0),沿AC所在直线将△ABC翻折使点B落在点D处,抛物线y=ax2+bx+c经过A、C、D三点.
如图所示,在平面直角坐标系中,△ABC的顶点坐标分别为点A(0,3)、B(-4,0)、C(1,0),沿AC所在直线将△ABC翻折使点B落在点D处,抛物线y=ax2+bx+c经过A、C、D三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均剪成四个小长方形,然后按图乙所示拼成一个大正方形.
图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均剪成四个小长方形,然后按图乙所示拼成一个大正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,羊年春节到了,小明亲手制作了3张一样的卡片,在每张卡片上分别写上“新”“年”“好”三个字,并随机放入一个不透明的信封中,然后让小芳分三次从信封中摸3张卡片(每次摸1张,摸出不放回).
如图,羊年春节到了,小明亲手制作了3张一样的卡片,在每张卡片上分别写上“新”“年”“好”三个字,并随机放入一个不透明的信封中,然后让小芳分三次从信封中摸3张卡片(每次摸1张,摸出不放回).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com