
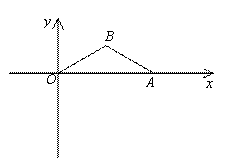
已知:如图,在平面直角坐标系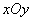 中,抛物线
中,抛物线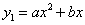 过点A(6,0)和点B(3,
过点A(6,0)和点B(3, ).
).
(1)求抛物线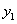 的解
的解 析式;
析式;
(2)将抛物线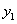 沿x轴翻折得抛物线
沿x轴翻折得抛物线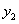 ,求抛物线
,求抛物线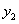 的解析式;
的解析式;
(3)在(2)的条件下,抛物线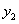 上是否存在点M,使
上是否存在点M,使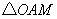 与
与 相似?如果存在,求出点M的坐标;如果不存在,说明理由.
相似?如果存在,求出点M的坐标;如果不存在,说明理由.
解:(1)依题意,得 解得
解得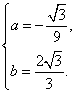
∴抛物线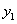 的解析式为
的解析式为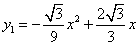 .
.
(2)将抛物线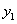 沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点
沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点 .
.
设抛物线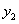 的解析式为
的解析式为 ,
,
∴ 解得
解得
∴抛物线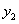 的解析式为
的解析式为 .
.
(3)过点B作BC⊥x轴于点C,
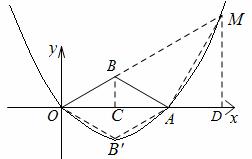 则有
则有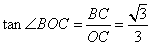 .
.
∴ ,
, .
.
∵OC=3,OA=6,
∴AC=3.
∴ ,
, .[来源:Z*xx*k.Com]
.[来源:Z*xx*k.Com]
∴OB=AB.
即 是顶角为120º的等腰三角形.
是顶角为120º的等腰三角形.
分两种情况:
①当点M在x轴下方时,
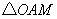 就是
就是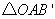 ,此时点M的坐标为
,此时点M的坐标为 .
.
②当点M在x轴上方时,假设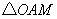
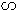
 ,
,
则有AM=OA=6,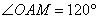 .
.
过点M作MD⊥x轴于点D,则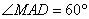 .
.
∴ ,
,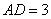 . ∴OD=9.
. ∴OD=9.
而(9, )满足关系式
)满足关系式 ,
,
即点M在抛物线 上.
上.
根据对称性可知,点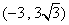 也满足条件.
也满足条件.
综上所述,点M的坐标为 ,
, ,
, .
.


科目:初中数学 来源: 题型:
在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m2)与体积V(单位:m3)满足函数关系式 (k为常数,k
(k为常数,k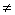 0),其图象如图所示,则k的值为( )
0),其图象如图所示,则k的值为( )
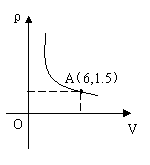

A.9 B.-9 C.4 D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
中踏销售某种商品,每件进价为10元,在销售过程中发现,平均每天的销售量
y(件)与销售价x(元/件)之间的关系可近似的看做一次函数: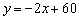 ;
;
 (1)求中踏平均每天销售这种商品的利润w(元)与销售价x之间的函数关系式;
(1)求中踏平均每天销售这种商品的利润w(元)与销售价x之间的函数关系式;
(2)当这种商 品的销售价为多少元时,可以获得最大利润?最大利润是多少?
品的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数 (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;

查看答案和解析>>
科目:初中数学 来源: 题型:
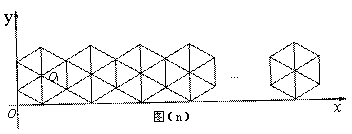
我们把图(1)称作正六边形的基 本图,将此基本图不断复制并平移,使得相邻两个基本图的一边重合,这样得到图(2),图(3),…,
本图,将此基本图不断复制并平移,使得相邻两个基本图的一边重合,这样得到图(2),图(3),…,
如此进行下去,直至得图(n).
 |
图(1)  图(2) 图(3)
图(2) 图(3)
(1)将图(n)放在直角坐标系中,设其中第一个基本图的对称中心O1的坐标为(x1 ,4),则x1 = ;
(2)图(n)的对称中心的横坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
某项工作,甲单独做要4天完成,乙单独做要6天完成,若甲先做1天后,然后甲、乙合作完成此项工作,若设甲一共做了x天,所列方程是( ).
A.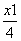 +
+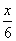 =1 B.
=1 B. +
+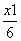 =1
=1
C. +
+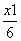 =1 D.
=1 D. +
+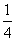 +
+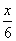 =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com