
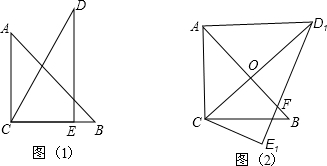
分析 (1)设D1E1与BC交于点G,求出∠CGE1,根据对顶角相等求出∠FGB,即可解决问题.
(2)首先证明OA=OC,∠AOC=90°,在Rt△AOD中,利用勾股定理即可解决问题.
(3)设直线CB交D2E2于点M,求出CM与BC比较即可判断.
解答 解:(1)设D1E1与BC交于点G,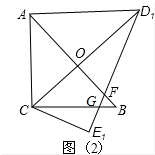
在Rt△CE1G中,∠GCE1=15°,
∴∠CGE1=75°,
∴∠FGB=∠CGE1=75°,又∠B=45°,
∴∠OFD1=∠BFG=60°
(2)由旋转知∠ACO=45°,
∴∠CAO=∠ACO=45°,∠AOC=90°,
∴AO=OC=$\frac{1}{2}$AB=5cm,
∴OD1=12cm,可证∠AOD1=∠AOC=90°,
在Rt△AOD1中,AD1=$\sqrt{O{A}^{2}+O{{D}^{2}}_{1}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13cm
(3)设直线CB交D2E2于点M,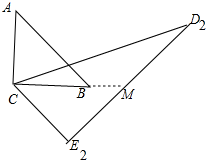
∴∠MCE2=45°,∠E2=90°,
∴CE2=ME2=$\frac{17}{2}$,
∴CM=$\frac{17}{2}$$\sqrt{2}$,
而CB=5$\sqrt{2}$<CM,
故点B在△D2CE2的内部.
点评 本题考查旋转的性质、等腰直角三角形的判定和性质、勾股定理等知识,解题的关键是理解旋转角的定义,灵活运用这些知识解决问题,属于中考常考题型.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
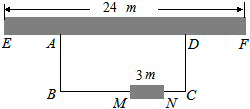 如图,利用一面墙(墙EF最长可利用24米),围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图MN所示,不用砌墙),用46米长的墙的材料做围墙,设这个苗圃园垂直于墙的一边的长为x米.
如图,利用一面墙(墙EF最长可利用24米),围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图MN所示,不用砌墙),用46米长的墙的材料做围墙,设这个苗圃园垂直于墙的一边的长为x米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的偏差(单位:克) | -3 | -2 | 0 | +1 | +1.5 | +2.5 |
| 袋数(单位:袋) | 1 | 4 | 3 | 4 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com