
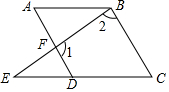
 如图,已知∠A=∠C,∠1与∠2互补,求证:AB∥CD.
如图,已知∠A=∠C,∠1与∠2互补,求证:AB∥CD. 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
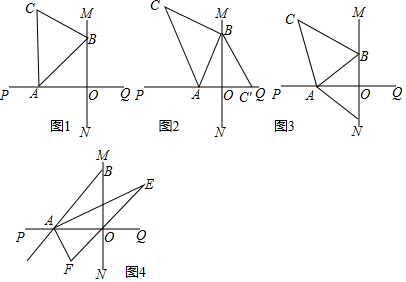
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
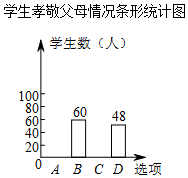 某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:| 选项 | 频数 | 频率 |
| A | m | 0.15 |
| B | 60 | p |
| C | n | 0.4 |
| D | 48 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com