
 ij�����п��ý�ѧ�ĸ��ѧ���ֳ�5��ѧϰС�飬��ȡ�������ķ�ʽ����ͼ������ijУ�ˣ�1������Ҽ�ͼ����A��B��C��D��E�ֱ�������ѧϰС���λ�ã���֪A�������Ϊ��-1��3����
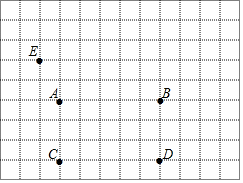
ij�����п��ý�ѧ�ĸ��ѧ���ֳ�5��ѧϰС�飬��ȡ�������ķ�ʽ����ͼ������ijУ�ˣ�1������Ҽ�ͼ����A��B��C��D��E�ֱ�������ѧϰС���λ�ã���֪A�������Ϊ��-1��3�������� ��1������A�������Ϊ��-1��3�������ɵõ�ƽ��ֱ������ϵ���ݴ˵ó���������ѧϰС������ꣻ
��2������ƽ���ߵ����ʣ��Լ�������������ʣ����ɵõ���FAB����AFO����FOD֮��ĵ�����ϵ��
��� �⣺��1����������ϵ��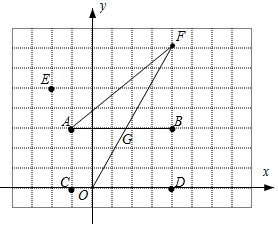
��ͼ�ɵã�B��4��3����C��-1��0����D��4��0����E��-2��5����
��2����AB��OD��
���FOD=��FGB��
�ߡ�FGB�ǡ�AFG����ǣ�
���FGB=��FAB+��AFO��
���FOD=��FAB+��AFO��
�ʴ�Ϊ����FOD=��FAB+��AFO��
���� ������Ҫ����������ȷ��λ���Լ�ƽ���ߵ����ʵ����ã�����ʱע�⣺��ֱ��ƽ�У�ͬλ����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���B=30�㣬��C=45�㣬AB=8����AC��BC�ij��ȣ�����������ţ���
��ͼ���ڡ�ABC�У���B=30�㣬��C=45�㣬AB=8����AC��BC�ij��ȣ�����������ţ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+2��x�ᡢy��ֱ��ཻ�ڵ�A��B���ı���ABCD�������Σ�˫����y=$\frac{k}{x}$ �ڵ�һ��������D��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+2��x�ᡢy��ֱ��ཻ�ڵ�A��B���ı���ABCD�������Σ�˫����y=$\frac{k}{x}$ �ڵ�һ��������D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
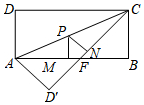 ��ͼ������ABCD�У�AB=8��BC=4������ADC��AC�۵�����D���ڵ�D�䴦��CD����AB���ڵ�F��
��ͼ������ABCD�У�AB=8��BC=4������ADC��AC�۵�����D���ڵ�D�䴦��CD����AB���ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С�Ŷ�������ѧУ��ͬѧʹ���ֻ�����������˵��飬�����ݵ���Ľ����������ͼ��ʾ��ͳ��ͼ����ͼ��֪�������ֻ�����Ϸ��ͬѧռ30%���������ֻ�����ѧϰ��ͬѧ���ڵ����ε�Բ�ĽǵĶ�����72�㣮
С�Ŷ�������ѧУ��ͬѧʹ���ֻ�����������˵��飬�����ݵ���Ľ����������ͼ��ʾ��ͳ��ͼ����ͼ��֪�������ֻ�����Ϸ��ͬѧռ30%���������ֻ�����ѧϰ��ͬѧ���ڵ����ε�Բ�ĽǵĶ�����72�㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com