练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=6，则四边形CODE的周长为12．

    分析 由CE∥BD，DE∥AC，可证得四边形CODE是平行四边形，又由四边形ABCD是矩形，根据矩形的性质，易得OC=OD=3，即可判定四边形CODE是菱形，继而求得答案．

    解答 解：∵CE∥BD，DE∥AC，
    ∴四边形CODE是平行四边形，
    ∵四边形ABCD是矩形，
    ∴AC=BD=6，OA=OC，OB=OD，
    ∴OD=OC=$\frac{1}{2}$AC=3，
    ∴四边形CODE是菱形，
    ∴四边形CODE的周长为=4OC=4×3=12．
    故答案为：12．

    点评 此题考查了菱形的判定与性质以及矩形的性质．此题难度不大，注意证得四边形CODE是菱形是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届重庆市九年级3月月考数学试卷（解析版） 题型：填空题

    口袋里装有五个大小形状都相同，所标数字不同的小球，小球所标的数字分别是 -3，-2.5，-1，2，3，先随机抽取一个球得到的数字记为k，放回后再抽一个球得到的数字记为b ，则满足条件关于x的一次函数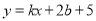的图象不经过第四象限的概率是_________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列给出的算式中，你认为可以帮助探究有理数加法法则的算式组合是（　　）
    ①3+（-2）；②4+3；③（-3）+（-2）；④3+13；⑤3+0；⑥6+（-3）；⑦4+（-5）；⑧5+（-5）．
    A．①②③④⑤⑧B．②③⑤⑥⑦⑧C．①③④⑤⑥⑧D．①②④⑤⑦⑧

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知x是$\sqrt{5}$的小数部分，则$\frac{{x}^{2}}{{x}^{2}-1}÷（\frac{1}{x-1}+1）$=$\frac{3-\sqrt{5}}{4}$．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年浙江省八年级3月月考数学试卷（解析版） 题型：单选题

    小明在计算时遇到以下情况，结果正确的是（ ）

    A. B.

    C. D. 以上都不是

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，AB∥CD，∠E=120°，∠F=90°，∠A+∠C的度数是（　　）
    A．30°B．35°C．40°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．化简
    （1）$\frac{a-2}{a+1}-\frac{2a-3}{a+1}$
    （2）$\frac{3-a}{2a-4}÷（{a+2-\frac{5}{a-2}}）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．将一个正方体沿某些棱展开后，能够得到的平面图形是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：
    （1）3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$÷2$\sqrt{3}$
    （2）（3+2$\sqrt{3}$）（2$\sqrt{3}$-3）-（2$\sqrt{3}$-1）2．

    查看答案和解析>>

    同步练习册答案