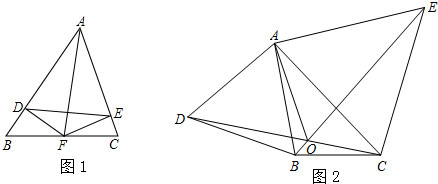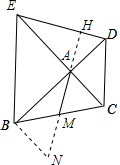
解:(1)如图,延长AM到N,使AM=MN,连接BN,延长MA交DE于H,
易证△BMN≌△CMA,
则BN=AC=AD,∠ABN=∠ABC+∠CBN=∠ABC+∠ACB=90°,
所以,△ADE≌△ACB,
所以,ED=AN=2AM,
故答案为:ED=2AM,AM⊥ED;
(2)ED=2AM,AM⊥ED;
证明:延长AM到N,使MN=AM,连BN,则ABNC是平行四边形.
∴AC=BN,∠ABN+∠BAC=180°
又∵∠DAE+∠BAC=180°,
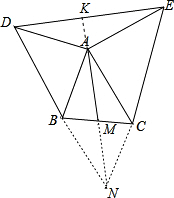
∴∠ABN=∠DAE.
再证:△DAE≌△ABN
∴DE=2AM,∠BAN=∠EDA.
延长MN交DE于K,
∵∠BAN+∠DAK=90°,
∴∠KDA+∠DAK=90°.
∴AM⊥ED.
(3)ED=2AM,AM⊥ED.
分析:(1)ED=2AM,AM⊥ED.由于△ABC是直角三角形,根据已知条件和斜边上的中线等于斜边的一半就可以得到ED=BC=2AM,然后利用斜边上的中线的性质和已知条件可以证明AM⊥ED;
(2)ED=2AM,AM⊥ED.延长AM到N,使MN=AM,连BN,则ABNC是平行四边形,再结合已知条件可以证明△DAE≌△ABN,根据全等三角形的性质可以得到DE=2AM,∠BAN=∠EDA,再延长MN交DE于K,因为∠BAN+∠DAK=90°,所以∠KDA+∠DAK=90°这样就证明了AM⊥ED;
(3)ED=2AMAM⊥ED.根据(2)的证明过程可以知道,结论和等腰直角△ABE和△ACD的位置没有关系,仍然可以得到△DAE≌△ABN,也即仍然结论成立.
点评:本题综合考查了三角形全等的判定和平行四边形的判定,此题是开放性试题,利用等腰直角三角形的性质进行探究,由特殊到一般最后得到一般图形变换的规律.

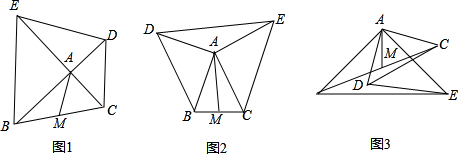
 解:(1)如图,延长AM到N,使AM=MN,连接BN,延长MA交DE于H,
解:(1)如图,延长AM到N,使AM=MN,连接BN,延长MA交DE于H,


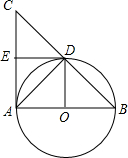 (2012•广州模拟)如图,以△ABC的边AB为直径的⊙O交边BC于点D,其中边AC与⊙O相切于点A,E为AC中点.
(2012•广州模拟)如图,以△ABC的边AB为直径的⊙O交边BC于点D,其中边AC与⊙O相切于点A,E为AC中点.