
【题目】已知:如图,在![]() 中,
中,![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() 交
交![]() 的外接圆于点
的外接圆于点![]() ,连接
,连接![]()
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
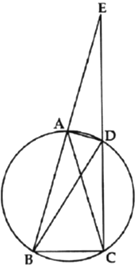
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据圆内接四边形的性质得到∠EDA=∠ABC,根据等腰三角形的性质得到∠ACB=∠ABC,等量代换得到∠ADB=∠EDA,于是得到结论;
(2)根据等腰三角形的性质得到∠ABC=∠ACB,∠ACD=∠E,求得∠BCE=90°,解直角三角形即可得到结论.
(1)∵四边形ABCD内接于圆,
∴∠EDA=∠ABC,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠EDA=∠ACB,
又∵∠ADB=∠ACB,
∴∠ADB=∠EDA,
∴AD平分∠BDE;
(2)∵AE=AB=AC,
∴∠ABC=∠ACB,∠ACD=∠E,
∵∠ABC+∠ACB+∠ACD+∠E=180°,
∴∠ACB+∠ACE=90°,
∴∠BCE=90°,
∵∠BDC=∠BAC=30°,BC=2,
![]() ,
,
∴CD =2![]() .
.


科目:初中数学 来源: 题型:
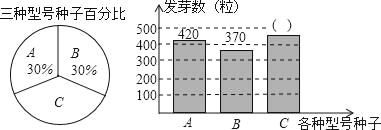
【题目】松山区种子培育基地用A,B,C三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图:
(1)求C型号种子的发芽数;
(2)通过计算说明,应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放在一起,从中随机取出一粒,求取到C型号发芽种子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
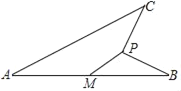
【题目】如图,线段AB=4,M为AB的中点,动点P到点M的距离是1,连接PB,线段PB绕点P逆时针旋转90°得到线段PC,连接AC,则线段AC长度的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.在Rt△ABC中,∠ACB=90°,AC=6,BC=8.点D是BC边上一点,连接AD,若△ABD是准互余三角形,则BD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
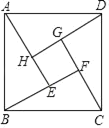
【题目】如图所示图案是我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为”赵爽弦图“.已知AE=4,BE=3,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳池每次换水前后水的体积基本保持不变,当该游泳池以每小时300立方米的速度放水时,经3小时能将池内的水放完.设放水的速度为x立方米/时,将池内的水放完需y小时.已知该游泳池每小时的最大放水速度为350立方米
(1)求y关于x的函数表达式.
(2)若该游泳池将放水速度控制在每小时200立方米至250立方米(含200立方米和250立方米),求放水时间y的范围.
(3)该游泳池能否在2.5小时内将池内的水放完?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《N家学生体质健康标准》规定:九年级男生坐位体前屈达到17.8厘米及以上为优秀;达到13.8厘米至17.7厘米为良好;达到-0.2厘米至13.7厘米为及格;达到-0.3厘米及以下为不及格,某校为了了解九年级男生的身体柔韧性情况,从该校九年级男生中随机抽取了20%的学生进行坐位体前屈测试,并把测试结果绘制成如图所示的统计表和扇形统计图(部分信息不完整),请根据所给信息解答下列问题.
某校九年级若干男生坐位体前屈成绩统计表
成绩(厘米) | 等级 | 人数 |
≥17.8 | 优秀 |
|
13.8~17.7 | 良好 |
|
0.2~13.7 | 及格 | 15 |
≤-0.3 | 不及格 |
|
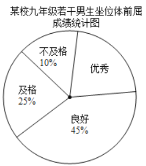
(1)求参加本次坐位体前屈测试的人数;
(2)求a,b,c的值;
(3)试估计该年级男生中坐位体前屈成绩不低于13.8厘米的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
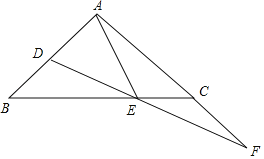
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF;
(2)判断BD和CF的数量关系,并说明理由;
(3)若AB=3,AE=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的方程x2+(3k+1)x+2k2+1=0的两个不相等实数根,且满足(x1﹣1)(x2﹣1)=8k2,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com