
如图,在矩形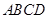 中,
中,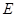 在
在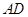 上,
上, ,交
,交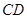 于
于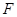 ,连结
,连结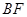 ,则图中与
,则图中与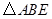 一定相似的三角形是
一定相似的三角形是
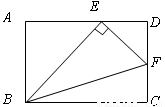
A.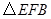 B.
B.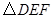 C.
C.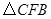 D.
D.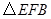 和
和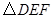
科目:初中数学 来源: 题型:
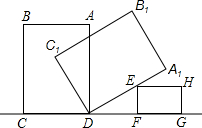 如图,在矩形ABCD中,已知AB=3cm,BC=4cm.将矩形ABCD绕着点D在桌面上顺时针旋转至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为
如图,在矩形ABCD中,已知AB=3cm,BC=4cm.将矩形ABCD绕着点D在桌面上顺时针旋转至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为查看答案和解析>>
科目:初中数学 来源:2013年辽宁省辽阳市高级中等学校招生考试数学 题型:044
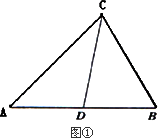
定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”
性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等,
理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O,
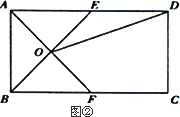
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积,
探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△![]() CD与△ABC重合部分的面积等于△ABC面积的
CD与△ABC重合部分的面积等于△ABC面积的![]() ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
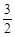 x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.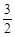 x+b平分矩形OABC的面积,求b的值;
x+b平分矩形OABC的面积,求b的值;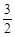 x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;查看答案和解析>>
科目:初中数学 来源:2013届山东省济南市长清区九年级学业水平模拟考试数学试卷(带解析) 题型:单选题
如图,在矩形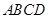 中,
中,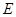 在
在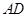 上,
上,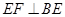 ,交
,交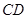 于
于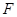 ,连结
,连结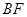 ,则图中与
,则图中与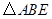 一定相似的三角形是
一定相似的三角形是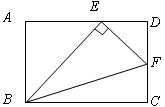
A.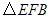 | B.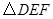 | C.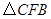 | D.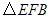 和 和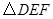 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com