
°æƒø°ø¡‚–ŒABCD‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–µƒŒª÷√»ÁÕºÀ˘ 棨∂‘Ω«œþAC”ÎBDµƒΩªµ„E«°∫√‘⁄y÷·…œ£¨π˝µ„D∫ÕBCµƒ÷–µ„Hµƒ÷±œþΩªAC”⁄µ„F£¨œþ∂ŒDE£¨CDµƒ≥§ «∑Ω≥Ãx2©Å9x+18=0µƒ¡Ω∏˘£¨«ÎΩ‚¥œ¬¡–Œ £∫
£®1£©«Ûµ„Dµƒ◊¯±Í£ª
£®2£©»Ù∑¥±»¿˝∫Ø ˝y=![]() £®k°Ÿ0£©µƒÕºœÛæ≠π˝µ„H£¨‘Úk=°° °°£ª
£®k°Ÿ0£©µƒÕºœÛæ≠π˝µ„H£¨‘Úk=°° °°£ª
£®3£©µ„Q‘⁄÷±œþBD…œ£¨‘⁄÷±œþDH…œ «∑ҥʑ⁄µ„P£¨ π“‘µ„F£¨C£¨P£¨QŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Pµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ

°æ¥∞∏°ø£®1£©£®©Å![]() £¨3
£¨3![]() £©£®2£©
£©£®2£©![]() £®3£©£®
£®3£©£®![]() £¨
£¨![]() £©ªÚ£®©Å
£©ªÚ£®©Å![]() £¨5
£¨5![]() £©ªÚ£®
£©ªÚ£®![]() £¨©Å
£¨©Å![]() £©
£©
°æΩ‚Œˆ°ø
£®1£©”…œþ∂ŒDE£¨CDµƒ≥§ «∑Ω≥Ãx2©Å9x+18=0µƒ¡Ω∏˘£¨«“CD£æDE£¨ø…«Û≥ˆCD°¢DEµƒ≥§£¨”…Àƒ±þ–ŒABCD «¡‚–Œ£¨¿˚”√¡‚–Œµƒ–‘÷ ø…«Ûµ√Dµ„µƒ◊¯±Í.
(2)”…£®1£©ø…µ√OB°¢CM£¨ø…µ√B°¢C◊¯±Í£¨Ω¯∂¯«Ûµ√Hµ„◊¯±Í£¨”…∑¥±»¿˝∫Ø ˝y=![]() £®k°Ÿ0£©µƒÕºœÛæ≠π˝µ„H£¨ø…«Ûµƒkµƒ÷µ;
£®k°Ÿ0£©µƒÕºœÛæ≠π˝µ„H£¨ø…«Ûµƒkµƒ÷µ;
(3)∑÷±“‘CFŒ™∆Ω––Àƒ±þ–Œµƒ“ª±þªÚ’þŒ™∂‘Ω«œþµƒ«È–ŒΩ¯––Ã÷¬€º¥ø….
£®1£©x2©Å9x+18=0£¨
£®x©Å3£©£®x©Å6£©=0£¨
x=3ªÚ6£¨
°þCD£æDE£¨
°ýCD=6£¨DE=3£¨
°þÀƒ±þ–ŒABCD «¡‚–Œ£¨
°ýAC°ÕBD£¨AE=EC=![]() =3
=3![]() £¨
£¨
°ý°œDCA=30°„£¨°œEDC=60°„£¨
Rt°˜DEM÷–£¨°œDEM=30°„£¨
°ýDM=![]() DE=
DE=![]() £¨
£¨
°þOM°ÕAB£¨
°ýS¡‚–ŒABCD=![]() ACBD=CDOM£¨
ACBD=CDOM£¨
°ý![]() =6OM£¨OM=3
=6OM£¨OM=3![]() £¨
£¨
°ýD£®©Å![]() £¨3
£¨3![]() £©£ª
£©£ª
£®2£©°þOB=DM=![]() £¨CM=6©Å
£¨CM=6©Å![]() =
=![]() £¨
£¨
°ýB£®![]() £¨0£©£¨C£®
£¨0£©£¨C£®![]() £¨3
£¨3![]() £©£¨
£©£¨
°þH «BCµƒ÷–µ„£¨
°ýH£®3£¨![]() £©£¨
£©£¨
°ýk=3°¡![]() =
=![]() £ª
£ª
π ¥∞∏Œ™£∫![]() £ª
£ª
£®3£©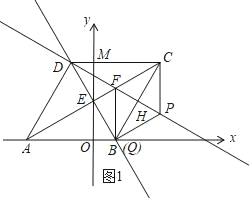
¢Ÿ°þDC=BC£¨°œDCB=60°„£¨
°ý°˜DCB «µ»±þ»˝Ω«–Œ£¨
°þH «BCµƒ÷–µ„£¨
°ýDH°ÕBC£¨
°ýµ±Q”ÎB÷ÿ∫œ ±£¨»ÁÕº1£¨Àƒ±þ–ŒCFQP «∆Ω––Àƒ±þ–Œ£¨
°þFC=FB£¨
°ý°œFCB=°œFBC=30°„£¨
°ý°œABF=°œABC©Å°œCBF=120°„©Å30°„=90°„£¨
°ýAB°ÕBF£¨CP°ÕAB£¨
Rt°˜ABF÷–£¨°œFAB=30°„£¨AB=6£¨
°ýFB=2![]() =CP£¨
=CP£¨
°ýP£®![]() £¨
£¨![]() £©£ª
£©£ª
¢⁄
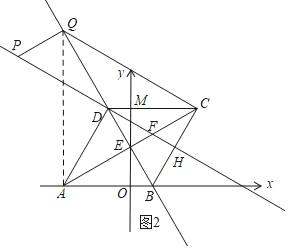
»ÁÕº2£¨°þÀƒ±þ–ŒQPFC «∆Ω––Àƒ±þ–Œ£¨
°ýCQ°ŒPH£¨
”…¢Ÿ÷™£∫PH°ÕBC£¨
°ýCQ°ÕBC£¨
Rt°˜QBC÷–£¨BC=6£¨°œQBC=60°„£¨
°ý°œBQC=30°„£¨
°ýCQ=6![]() £¨
£¨
¡¨Ω”QA£¨
°þAE=EC£¨QE°ÕAC£¨
°ýQA=QC=6![]() £¨
£¨
°ý°œQAC=°œQCA=60°„£¨°œCAB=30°„£¨
°ý°œQAB=90°„£¨
°ýQ£®©Å![]() £¨6
£¨6![]() £©£¨
£©£¨
”…¢Ÿ÷™£∫F£®![]() £¨2
£¨2![]() £©£¨
£©£¨
”…FµΩCµƒ∆Ω“∆πʬ…ø…µ√PµΩQµƒ∆Ω“∆πʬ…£¨‘ÚP£®©Å![]() ©Å3£¨6
©Å3£¨6![]() ©Å
©Å![]() £©£¨º¥P£®©Å
£©£¨º¥P£®©Å![]() £¨5
£¨5![]() £©£ª
£©£ª
¢€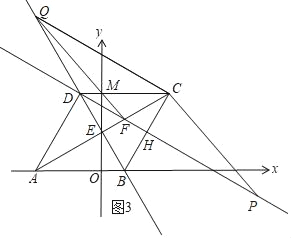
»ÁÕº3£¨Àƒ±þ–ŒCQFP «∆Ω––Àƒ±þ–Œ£¨
Õ¨¿Ì÷™£∫Q£®©Å![]() £¨6
£¨6![]() £©£¨F£®
£©£¨F£®![]() £¨2
£¨2![]() £©£¨C£®
£©£¨C£®![]() £¨3
£¨3![]() £©£¨
£©£¨
°ýP£®![]() £¨©Å
£¨©Å![]() £©£ª
£©£ª
◊€…œÀ˘ ˆ£¨µ„Pµƒ◊¯±ÍŒ™£∫£®![]() £¨
£¨![]() £©ªÚ£®©Å
£©ªÚ£®©Å![]() £¨5
£¨5![]() £©ªÚ£®
£©ªÚ£®![]() £¨©Å
£¨©Å![]() £©£Æ
£©£Æ


 ◊÷¥ æ‰∂Œ∆™œµ¡–¥∞∏
◊÷¥ æ‰∂Œ∆™œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∞—±þ≥§Œ™3µƒ’˝∑Ω–Œ![]() »∆µ„AÀ≥ ±’Ζ˝◊™45°„µ√µΩ’˝∑Ω–Œ
»∆µ„AÀ≥ ±’Ζ˝◊™45°„µ√µΩ’˝∑Ω–Œ![]() £¨±þ
£¨±þ![]() ”Î
”Î![]() Ωª”⁄µ„O£¨‘ÚÀƒ±þ–Œ
Ωª”⁄µ„O£¨‘ÚÀƒ±þ–Œ![]() µƒ÷Ð≥§ «£® £©
µƒ÷Ð≥§ «£® £©

A. 6B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy£Ω©Å![]() x2©Åx+4”Îx÷·Ωª”⁄A£¨B¡Ωµ„(A‘⁄Bµƒ◊Û≤ý)£¨”Îy÷·Ωª”⁄µ„C£Æ
x2©Åx+4”Îx÷·Ωª”⁄A£¨B¡Ωµ„(A‘⁄Bµƒ◊Û≤ý)£¨”Îy÷·Ωª”⁄µ„C£Æ
(1)«Ûµ„A£¨µ„Bµƒ◊¯±Í£ª
(2)«Û°˜ABCµƒ√ʪ˝£ª
(3)PŒ™µ⁄∂˛œÛœÞ≈◊ŒÔœþ…œµƒ“ª∏ˆ∂ص„£¨«Û°˜ACP√ʪ˝µƒ◊Ó¥Û÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄’˝∑Ω–Œ![]() ÷–£¨µ„
÷–£¨µ„![]() «±þ
«±þ![]() …œ“ª∏ˆ∂ص„£¨¡¨Ω·
…œ“ª∏ˆ∂ص„£¨¡¨Ω·![]() £¨
£¨![]() £¨µ„
£¨µ„![]() £¨
£¨![]() ∑÷±Œ™
∑÷±Œ™![]() £¨
£¨![]() µƒ÷–µ„£¨¡¨Ω·
µƒ÷–µ„£¨¡¨Ω·![]() Ωª÷±œþ
Ωª÷±œþ![]() ”⁄µ„E£Æ
”⁄µ„E£Æ
£®1£©»ÁÕº1£¨µ±µ„![]() ”ε„
”ε„![]() ÷ÿ∫œ ±£¨
÷ÿ∫œ ±£¨![]() µƒ–Œ◊¥ «_____________________£ª
µƒ–Œ◊¥ «_____________________£ª
£®2£©µ±µ„![]() ‘⁄µ„Mµƒ◊Û≤ý ±£¨»ÁÕº2£Æ
‘⁄µ„Mµƒ◊Û≤ý ±£¨»ÁÕº2£Æ
¢Ÿ“¿Ã‚“‚≤π»´Õº2£ª
¢⁄≈–∂œ![]() µƒ–Œ◊¥£¨≤¢º”“‘÷§√˜£Æ
µƒ–Œ◊¥£¨≤¢º”“‘÷§√˜£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ±þ–ŒABCD÷–£¨∂‘Ω«œþAC”ÎBDœýΩª”⁄µ„O£¨AC∆Ω∑÷°œDAB£¨«“°œDAC=°œDBC£¨ƒ«√¥œ¬¡–Ω·¬€≤ª“ª∂®’˝»∑µƒ «£®°°°°£©

A. °˜AOD°◊°˜BOC B. °˜AOB°◊°˜DOC C. CD=BC D. BCCD=ACOA
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™‘⁄æÿ–ŒABCD÷–£¨AB=2£¨AD=4£ÆP «∂‘Ω«œþBD…œµƒ“ª∏ˆ∂ص„£®µ„P≤ª”ε„B°¢D÷ÿ∫œ£©£¨π˝µ„P◊˜PF°ÕBD£¨Ωª…‰œþBC”⁄µ„F£Æ¡™Ω·AP£¨ª≠°œFPE=°œBAP£¨PEΩªBF”⁄µ„E£Æ…ËPD=x£¨EF=y£Æ
£®1£©µ±µ„A°¢P°¢F‘⁄“ªÃı÷±œþ…œ ±£¨«Û°˜ABFµƒ√ʪ˝£ª
£®2£©»ÁÕº1£¨µ±µ„F‘⁄±þBC…œ ±£¨«Ûyπÿ”⁄xµƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢–¥≥ˆ∫Ø ˝∂®“”ڣª
£®3£©¡™Ω·PC£¨»Ù°œFPC=°œBPE£¨«Î÷±Ω”–¥≥ˆPDµƒ≥§£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ€≤Ïœ¬¡–µ» Ω£∫
µ⁄1∏ˆµ» Ω£∫a1=![]()
µ⁄2∏ˆµ» Ω£∫a2=![]()
µ⁄3∏ˆµ» Ω£∫a3=![]()
µ⁄4∏ˆµ» Ω£∫a4=![]()
°≠°≠
«Îªÿ¥œ¬¡–Œ £∫
£®1£©∞¥…œ ˆµ» Ωµƒπʬ…£¨¡–≥ˆµ⁄5∏ˆµ» Ω£∫a5=°° °°=°° °°
£®2£©”√∫¨nµƒ Ω◊”±Ì æµ⁄n∏ˆµ» Ω£∫an=°° °°=°° °°
£®3£©«Ûa1+a2+a3+a4+°≠+a2017µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝÷·…œ»˝µ„M£¨O£¨N∂‘”¶µƒ ˝∑÷± «-1£¨0£¨3£¨µ„PŒ™ ˝÷·…œ»Œ“‚µ„£¨∆‰∂‘”¶µƒ ˝Œ™x.»Áπ˚µ„P“‘√ø∑÷÷”1∏ˆµ•Œª≥§∂»µƒÀŸ∂»¥”µ„OœÚ◊Û‘À∂Ø£¨Õ¨ ±µ„M∫Õµ„N∑÷±“‘√ø∑÷÷”2∏ˆµ•Œª≥§∂»∫Õ√ø∑÷÷”3∏ˆµ•Œª≥§∂»µƒÀŸ∂»“≤œÚ◊Û‘À∂أƅËt∑÷÷” ±Pµ„µΩµ„M°¢µ„Nµƒæý¿Îœýµ»£¨‘Útµƒ÷µŒ™_______.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∑Áæ∞«¯º∆ªÆ‘⁄¬ÃªØ«¯”Ú÷÷÷≤“¯–” ˜£¨œ÷º◊°¢““¡Ωº“”–œýÕ¨µƒ“¯–” ˜√Áø…π©—°‘Ò£¨∆‰æþÃÂœ˙ €∑Ω∞∏»Áœ¬£∫
º◊ | ““ | ||
π∫ ˜√Á ˝¡ø | œ˙ €µ•º€ | π∫ ˜√Á ˝¡ø | œ˙ €µ•º€ |
≤ª≥¨π˝500ø√ ± | 800‘™/ø√ | ≤ª≥¨π˝1000ø√ ± | 800‘™/ø√ |
≥¨π˝500ø√µƒ≤ø∑÷ | 700‘™/ø√ | ≥¨π˝1000ø√µƒ≤ø∑÷ | 600‘™/ø√ |
…Ëπ∫¬Ú“¯–” ˜√Áxø√£¨µΩ¡Ωº“π∫¬ÚÀ˘–Ë∑—”√∑÷±Œ™yº◊‘™°¢y““‘™
(1)∏√∑Áæ∞«¯–Ë“™π∫¬Ú800ø√“¯–” ˜√Á£¨»Ù∂º‘⁄º◊º“π∫¬ÚÀ˘“™∑—”√Œ™°° °°‘™£¨»Ù∂º‘⁄““º“π∫¬ÚÀ˘–Ë∑—”√Œ™°° °°‘™£ª
(2)µ±x£æ1000 ±£¨∑÷±«Û≥ˆyº◊°¢y““”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ª
(3)»Áπ˚ƒ„ «∏√∑Áæ∞«¯µƒ∏∫‘»À£¨π∫¬Ú ˜√Á ±”– ≤√¥∑Ω∞∏£¨Œ™ ≤√¥£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com