练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．下列说法中正确的是（　　）
    A．带根号的数都是无理数B．$\frac{π}{3}$是分数
    C．无理数是无限小数D．无限小数是无理数

    分析 无理数是指无限不循环小数，根据无理数的定义判断即可．

    解答 解：A、如$\sqrt{4}$=2是有理数不是无理数，故A选项错误；
    B、$\frac{π}{3}$不是分数，是无理数，故B选项错误；
    C、无理数都是无限小数，故C选项正确；
    D、无限不循环小数是无理数，无限循环小数是有理数，故D选项错误；
    故选：C．

    点评 此题主要考查了实数、无理数、有理数之间的关系，有理数都可以化为小数，其中整数可以看作小数点后面是零的小数，分数都可以化为有限小数或无限循环小数；无理数是无限不循环小数，其中有开方开不尽的数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

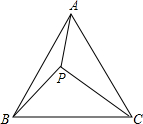    15．数学探究课上老师处这样一道题：“如图，等边△ABC中有一点P，且PA=3，PB=4，PC=5，试求∠APB的度数．”小明和小军探讨时发现了一种求∠APB度数的方法，下面是这种方法的一部分思路，请按照下列思路要求画图或判断
    （1）在图中画出△APC绕点A顺时针旋转60°后的△AP1B；
    （2）试判断△AP1P的形状，并说明理由；
    （3）试判断△BP1P的形状，并说明理由；
    （4）由（2）、（3）两问可知：∠APB=150°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，AD、AE、AF分别是△ABC的中线、角平分线和高，请你指出图中相等的角及相等的线段．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．一个多项式加上-2x3+4x2y+5y3后，得x3-x2y+3y2，求这个多项式，并求当x=y=-$\frac{1}{2}$时，这个多项式的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如果（a+1）2+|b-2|=0，求a2010+（a+b）2011的值是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算题
    （1）$\sqrt{625}-\sqrt{\frac{36}{169}}×\sqrt{0.25}$
    （2）$\root{3}{216}$+$\root{3}{-1000}$+$\sqrt{（-\frac{2}{3}）^{2}}$
    （3）（$\sqrt{2}$）2-$\sqrt{（-4）^{2}}$+4×$\root{3}{\frac{1}{8}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．阅读下列材料：
    小华遇到这样一个问题，如图1，△ABC中，∠ACB=30°，BC=6，AC=5，在△ABC内部有一点P，连接PA、PB、PC，求PA+PB+PC的最小值．
    小华是这样思考的：要解决这个问题，首先应想办法将这三条端点重合于一点的线段分离，然后再将它们连接成一条折线，并让折线的两个端点为定点，这样依据“两点之间，线段最短”，就可以求出这三条线段和的最小值了．他先后尝试了翻折、旋转、平移的方法，发现通过旋转可以解决这个问题．他的做法是，如图2，将△APC绕点C顺时针旋转60°，得到△EDC，连接PD、BE，则BE的长即为所求．
    （1）请你写出图2中，PA+PB+PC的最小值为$\sqrt{61}$；
    （2）参考小华的思考问题的方法，解决下列问题：
    ①如图3，菱形ABCD中，∠ABC=60°，在菱形ABCD内部有一点P，请在图3中画出并指明长度等于PA+PB+PC最小值的线段（保留画图痕迹，画出一条即可）；
    ②若①中菱形ABCD的边长为4，请直接写出当PA+PB+PC值最小时PB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．把下列各数分别填入相应的集合里．
    3，-7，-$\frac{2}{3}$，5.$\stackrel{•}{6}$，0，-8$\frac{1}{4}$，15，$\frac{1}{9}$
    （1）分数集合：{-$\frac{2}{3}$，5.$\stackrel{•}{6}$，-8$\frac{1}{4}$，$\frac{1}{9}$…}    （2）负数集合：{-7，-$\frac{2}{3}$，-8$\frac{1}{4}$，$\frac{1}{9}$…}   
    （3）整数集合：{3，-7，0，15…}    （4）非负数集合：{3，5.$\stackrel{•}{6}$，0，15，$\frac{1}{9}$…}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．化简下列各数前的符号：
    （1）-[-（-9）]；                 
    （2）-[+（-75）]．

    查看答案和解析>>

    同步练习册答案