
【题目】观察如图图形:
它们是按一定规律排列的:
(1)依照此规律,第8个图形共有__枚五角星.
(2)用代数式表示第n个图形共有___枚五角星
(3)第99个图形共有多少枚五角星?
【答案】(1)25;(2)3n+1;(3)298;
【解析】
(1)根据图形可知,每一副图比前一副图多3粒星,按此规律即可求出答案.
(2)根据图形可知,每一副图比前一副图多3粒星,按此规律即可求出答案.
(3)根据图形可知,每一副图比前一副图多3粒星,按此规律即可求出答案.
由题意可知:
(1)n=1,3×1+1=4;
n=2, 3×2+1=7;
n=3, 3×3+1=10;
n=4, 3×4+1=13;
∴第8个图形共有25枚;
(2)n=1时,有4枚,
n=2时,有4+3枚,
n=3时,由4+2×3枚,
如此类推,第n个图共有(3n+1)枚;
(3)当n=99时,3n+1=3×99+1=298枚.
故答案为(1)25;(2)3n+1;(3)298;


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如![]() 就是完全对称式(代数式中
就是完全对称式(代数式中![]() 换成b,b换成
换成b,b换成![]() ,代数式保持不变).下列三个代数式:①
,代数式保持不变).下列三个代数式:①![]() ;②
;②![]() ;③
;③![]() .其中是完全对称式的是( )
.其中是完全对称式的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+k﹣2经过点(m,n+1)和(m+1,2n+3),且﹣2<k<0,则n的取值范围是( )
A. ﹣2<n<0B. ﹣4<n<﹣2C. ﹣4<n<0D. 0<n<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F在矩形的边AD,BC上,点B与点D关于直线EF对称.设点A关于直线EF的对称点为G.
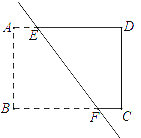
(1)画出四边形ABFE关于直线EF对称的图形;
(2)若∠FDC=16°,直接写出∠GEF的度数为 ;
(3)若BC=4,CD=3,写出求线段EF长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)请探究线段AF与FG的倍数关系,并证明你的结论。
(3)设FG=x,△EFG的面积为y,求y关于x的函数解析式,并直接写出x的取值范围;
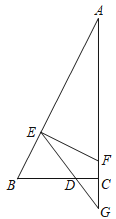
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述中,①所有的正数都是整数;②|a|一定是正数;③无限小数一定是无理数;④(-2)3没有平方根;⑤![]() 的平方根是±2.其中不正确的个数有( )
的平方根是±2.其中不正确的个数有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.

(1)分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);
(2)求A、B两城之间的距离,及t为何值时两车相遇;
(3)当两车相距300千米时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com