
分析 把问题转化为二次函数来解决:二次方程x2+mx+n=0与x2+px+q=0都有实根说明△>0,且其中任一方程的两根被另一方程的根分隔开来说明以y=x2+mx+n与y=x2+px+q两个函数有一个交点,由此联立方程组求得答案即可.
解答 解:如图,利用二次函数图象来解决,
由题意可知:①两个函数都与x轴有两个交点;
因此m2-4n>0,p2-4q>0;
②两个函数图象的交点在x轴的下方.
联立方程组:$\left\{\begin{array}{l}{y={x}^{2}+mx+n}\\{y={x}^{2}+px+q}\end{array}\right.$,
解得:x=$\frac{q-n}{m-p}$,y=$\frac{(q-n)^{2}}{(m-p)^{2}}$+m$\frac{q-n}{m-p}$+n,
当y<0时,即$\frac{(q-n)^{2}}{(m-p)^{2}}$+m$\frac{q-n}{m-p}$+n<0,
也就是(q-n)2+m(q-n)(m-p)-n(m-p)2<0.
综上所述,系数m、n、p、q应满足的条件是:
①m2-4n>0,p2-4q>0;②(q-n)2+m(q-n)(m-p)-n(m-p)2<0.
点评 此题考查根的判别式与一元二次方程根的情况,此题需要把方程转化为二次函数,利用二次函数与x轴的交点问题与函数的交点问题来解决.


科目:初中数学 来源: 题型:选择题
| A. | 若a=b,则a+c=b+c | B. | 若a+c=b+c,则a=b | C. | 若a=b,则ac=bc | D. | 若ac=bc,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
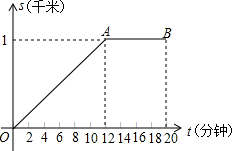 小明与小刚住在同一居民楼,小明早晨从家里出发匀速步行上学,小刚在小明出发10分钟后,匀速骑车按小明上学的路线去上学,结果在小明出发20分钟后他们同时到达学校.已知小明距离家的距离S(km)与小明出发时间t(分)的图象为图中的折线OA-AB.
小明与小刚住在同一居民楼,小明早晨从家里出发匀速步行上学,小刚在小明出发10分钟后,匀速骑车按小明上学的路线去上学,结果在小明出发20分钟后他们同时到达学校.已知小明距离家的距离S(km)与小明出发时间t(分)的图象为图中的折线OA-AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com