练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    四个连续自然数，中间两个数的积比前后两个数的积大2，证明这一结论是否正确．

    答案：
    解析：

    　　证明：设这四个连续自然数分别为：n、n＋1、n＋2、n＋3．

    　　则(n＋1)(n＋2)－n(n＋3)

    　　＝(n2＋n＋2n＋2)－(n2＋3n)

    　　＝n2＋3n＋2－n2－3n

    　　＝2．

    　　∴结论正确．

    　　分析：连续自然数可用含n的代数式表示出来：n、n＋1、n＋2、n＋3，再按题意求出两个积的差，即可证明结论的正确性．

    　　点拨：有关数的问题的解法关键是合理表示相关的数，再根据整式的相关运算性质进行计算．本题还可以用其他方式表示四个数：为n－1、n、n＋1、n＋2等．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

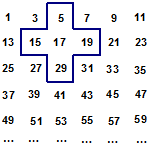    精英家教网将连续的奇数1，3，5，7，…，排成如图所示的数表，用十字框任意框出5个数．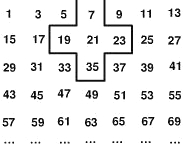
    探究规律一：设十字框中间的奇数为a，则框中五个奇数之和用含a的代数式表示为
     
    ．
    结论：这说明能被十字框框中的五个奇数之和一定是自然数p的奇数倍，这个自然数p是
     
    ．
    探究规律二：
    落在十字框中间且又是第二列的奇数是15，27，39…则这一列数可以用代数式表示为12m+3（m为正整数），同样，落在十字框中间且又是第三列，第四列，第五列的奇数分别可表示为
     
    ．
    运用规律：
    （1）已知被十字框框中的五个奇数之和为6025，则十字框中间的奇数是
     
    ．这个奇数落在从左往右第
     
    列．
    （2）请你写出一个不能够框在十字框中间的且大于500的奇数：
     
    ．
    （3）被十字框框中的五个奇数之和可能是485吗？可能是3045吗？说说你的理由．精英家教网
    变通运用：
    若把这些奇数重新排列如右图，解答下列问题：
    （1）下列能被十字框框在中间的奇数是（
     
    　）
    A.841   B.1121   C.1263  D.1091
    （2）被框在十字框中的五个数之和可能是1925吗？说说你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将连续的奇数1，3，5，7，…，排成如下图的数表，用图中所示的十字框可任意框出5个数．
    【探究规律一】：设十字框中间的奇数为a，则框中五个奇数之和用含a的代数式表示为
    5a
    5a
    ．
    【结论】：这说明能被十字框框中的五个奇数之和一定是自然数p的奇数倍，这个自然数p是
    5
    5
    ．
    【探究规律二】：落在十字框中间且又是第二列的奇数是15，27，39，51…则这一列数可以用代数式表示为12m+3（m为正整数），同样，落在十字框中间且又是第三列，第四列的奇数分别可表示为
    12m+5，13m+7
    12m+5，13m+7
    ．
    【运用规律】：
    （1）已知被十字框框中的五个奇数之和为6025，则十字框中间的奇数是
    1025
    1025
    ；这个奇数落在从左往右第
    3
    3
    列．
    （2）被十字框框中的五个奇数之和可能是485吗？可能是3045吗？说说你的理由．

    查看答案和解析>>

    科目：初中数学 来源：漫游数学世界八年级(上) 题型：044

    试应用整式运算，说明下列结论的正确性．

    (1)四个连续自然数中，中间两个数的积比首末两个数的积大；

    (2)四个连续自然数的积与1的和一定是平方数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

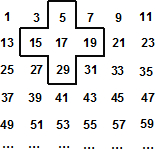
    将连续的奇数1，3，5，7，…，排成如图所示的数表，用十字框任意框出5个数．
    探究规律一：设十字框中间的奇数为a，则框中五个奇数之和用含a的代数式表示为______．
    结论：这说明能被十字框框中的五个奇数之和一定是自然数p的奇数倍，这个自然数p是______．
    探究规律二：
    落在十字框中间且又是第二列的奇数是15，27，39…则这一列数可以用代数式表示为12m+3（m为正整数），同样，落在十字框中间且又是第三列，第四列，第五列的奇数分别可表示为______．
    运用规律：
    （1）已知被十字框框中的五个奇数之和为6025，则十字框中间的奇数是______．这个奇数落在从左往右第______列．
    （2）请你写出一个不能够框在十字框中间的且大于500的奇数：______．
    （3）被十字框框中的五个奇数之和可能是485吗？可能是3045吗？说说你的理由．
    变通运用：
    若把这些奇数重新排列如右图，解答下列问题：
    （1）下列能被十字框框在中间的奇数是（______　）
    A.841　 B.1121　 C.1263　D.1091
    （2）被框在十字框中的五个数之和可能是1925吗？说说你的理由．

    查看答案和解析>>

    同步练习册答案