
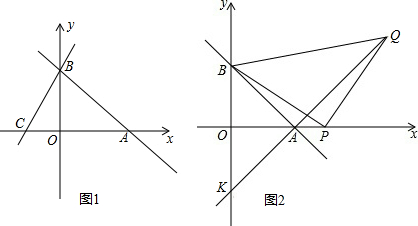
���� ��1������ȷ��B��C�������꣬���ô���ϵ�������ɽ�����⣻
��2�����ڣ���S��BDF=S��BDE����ֻ֪��DF=DE����DΪEF�е㣬���÷��������E��F�������꣬�����е����깫ʽ�г������鼴�ɽ�����⣻
��3��K���λ�ò������仯��ֻҪ֤��AC=CQ�������Ƴ���QAC=��OAK=45�㼴�ɽ�����⣻
��� �⣺��1����y=-x-b�ҹ���A��6��0����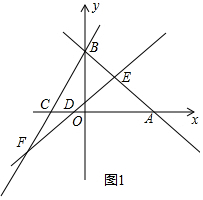
��-6-b=0��b=-6��
��y=-x+6��
��B��0��6����
��OB=6��
��OC��OB=1��3��
��OC=2��
��C��-2��0����
��y=kx+b������$\left\{\begin{array}{l}{-2k+b=0}\\{b=6}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=3}\\{b=6}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=3x+6��
��2���⣺���ڣ��������£���ͼ1�У�
��S��BDF=S��BDE��
��ֻ��DF=DE����DΪEF�е㣬
EΪֱ��AB��EF�Ľ���$\left\{\begin{array}{l}{y=-x+6}\\{y=\frac{1}{2}x-k}\end{array}\right.$���ɵ�$E��{\frac{2}{3}k+4\;��\;\;2-\frac{2}{3}k}��$��
FΪֱ��BC��EF�Ľ���$\left\{\begin{array}{l}{y=3x+6}\\{y=\frac{1}{2}x-k}\end{array}\right.$�ɵ�$F��{-\frac{2}{5}k-\frac{12}{5}\;��\;\;-\frac{6}{5}k-\frac{6}{5}}��$��
DΪx����EF�Ľ���D��2k��0����
�ߵ�DΪEF���е㣬
�����е㹫ʽ�ɵ�$��{2-\frac{2}{3}k}��+��{-\frac{6}{5}k-\frac{6}{5}}��=0$��
��k=$\frac{3}{7}$��
��3��K���λ�ò������仯���������£�
��ͼ2�У�����Q��CQ��x�ᣬ��PA=m��
�ߡ�POB=��PCQ=��BPQ=90�㣬
���OPB+��QPC=90�㣬��QPC+��PQC=90�㣬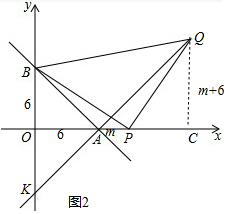
���OPB=��PQC��
��PB=PQ��
���BOP�ա�PCQ��
��BO=PC=6OP=CQ=6+m��
��AC=QC=6+m��
���QAC=��OAK=45�㣬
��OA=OK=6��
��K��0��-6����
���� ���⿼��һ�κ��������ʡ�����ֱ�������ε����ʺ��ж���ȫ�������ε��ж������ʡ���Ԫһ�η������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�ṹ�����̽�����⣬ѧ�����Ӹ����ߣ�����ȫ�������ν�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
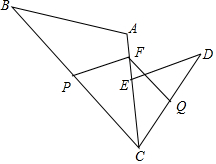 ��ͼ��E��A��C������ͬһ��ֱ���ϣ�������ABC��������CDE�Ƕ�����ȵĵ��������Σ�����BC��CDΪ���������εĵױߣ�F��AE���е㣬P��BC�ߵ��е㣬Q��CD�ߵ��е㣮
��ͼ��E��A��C������ͬһ��ֱ���ϣ�������ABC��������CDE�Ƕ�����ȵĵ��������Σ�����BC��CDΪ���������εĵױߣ�F��AE���е㣬P��BC�ߵ��е㣬Q��CD�ߵ��е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��AΪֱ�� | B�� | ��BΪֱ�� | C�� | ��CΪֱ�� | D�� | ����ֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�ı�BC=48cm����AD=16cm������EFGH�ı�FG��BC�ϣ�����E��H�ֱ���AB��AC�ϣ���������EF��FG�ı�Ϊ5��9�������EFGH���ܳ���
��ͼ����ABC�ı�BC=48cm����AD=16cm������EFGH�ı�FG��BC�ϣ�����E��H�ֱ���AB��AC�ϣ���������EF��FG�ı�Ϊ5��9�������EFGH���ܳ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com