
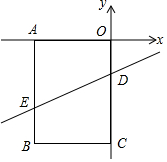
 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3),直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E,点P在矩形的边AB或BC上,作PF⊥ED于点F,连接PD,当△PFD是等腰三角形时,点P的坐标为(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$).
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3),直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E,点P在矩形的边AB或BC上,作PF⊥ED于点F,连接PD,当△PFD是等腰三角形时,点P的坐标为(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$). 分析 由于点P的位置不确定,所以需要分情况讨论,一是点P在AB边上,二是点P在BC边上,然后根据等腰三角形的性质即可求出P的坐标.
解答  解:当P在AB上时,
解:当P在AB上时,
设直线ED与x轴交于点G,
设PF=DF=x,
令y=0和x=-2代入y=$\frac{1}{2}$x-1
∴x=2和y=-2
∴G(2,0),E(-2,-2),
∴AG=4,AE=2,
∴tan∠PEF=$\frac{PF}{EF}$=$\frac{AG}{AE}=2$,
∴EF=$\frac{x}{2}$,
∴ED=x+$\frac{x}{2}$=$\frac{3x}{2}$,
令x=0代入y=$\frac{1}{2}$x-1,
∴D(0,-1)
∴ED=$\sqrt{(-2-0)^{2}+(-2+1)^{2}}$=$\sqrt{5}$
∴$\frac{3}{2}x$=$\sqrt{5}$,
∴x=$\frac{2\sqrt{5}}{3}$
∴由勾股定理可知:PE=$\frac{\sqrt{5}}{2}x$=$\frac{5}{3}$,
∴AP=AE-PE=2-$\frac{5}{3}$=$\frac{1}{3}$
此时P的坐标为(-2,-$\frac{1}{3}$)
当点P在BC边上时,
过点D作P′D⊥PD,垂足为D,
过点P作PH⊥y轴,垂足为H,
易证:△PDH∽△P′DC
∴$\frac{PH}{DH}=\frac{CD}{P′C}$
∵PH=2,DH=OD-OH=1-$\frac{1}{3}$=$\frac{2}{3}$
CD=OC-OD=3-1=2
∴$\frac{2}{\frac{2}{3}}=\frac{2}{P′C}$
∴P′C=$\frac{2}{3}$,
∴P′的坐标为(-$\frac{2}{3}$,-3)
故答案为:(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$)
点评 本题考查等腰三角形的性质,涉及相似三角形的判定与性质,勾股定理等知识,综合程度较高,需要学生灵活运用知识.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
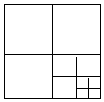 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2017}$ | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{1}{4}$)2017 | D. | 1-($\frac{1}{4}$)2017 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 研发组 | 管理组 | 操作组 | |
| 日工资(元/人) | 300 | 280 | 260 |
| 人数(人) | 3 | 4 | 5 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com