
【题目】点![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,且满足
,且满足![]() ,多项式
,多项式![]() 是五次四项式.
是五次四项式.
(1)![]() 的值为 ,
的值为 ,![]() 的值为 ,
的值为 ,![]() 的值为 .
的值为 .
(2)已知点![]() 是数轴上的两个动点,点
是数轴上的两个动点,点![]() 以每秒3个单位的速度向右运动,同时点
以每秒3个单位的速度向右运动,同时点![]() 从点
从点![]() 出发,以每秒7个单位的速度向左运动:
出发,以每秒7个单位的速度向左运动:
①若点![]() 从点
从点![]() 出发,点
出发,点![]() 和点
和点![]() 经过
经过![]() 秒后,在数轴上的点
秒后,在数轴上的点![]() 处相遇,求
处相遇,求![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
②若点![]() 先从点
先从点![]() 出发,运动到点
出发,运动到点![]() 处,点
处,点![]() 再出发,则点
再出发,则点![]() 运动几秒后两点之间的距离为5个单位长度?
运动几秒后两点之间的距离为5个单位长度?
【答案】(1)![]() 的值为-3,
的值为-3,![]() 的值为27,
的值为27,![]() 的值为-6;(2)①
的值为-6;(2)①![]() 的值为3,点
的值为3,点![]() 所表示的数是6;②点
所表示的数是6;②点![]() 运动3.5秒或4.5秒后两点之间的距离为5个单位长度
运动3.5秒或4.5秒后两点之间的距离为5个单位长度
【解析】
(1)根据平方和绝对值的非负性可以求出![]() 和
和![]() ,根据多项式的概念再求出
,根据多项式的概念再求出![]() ;
;
(2)①![]() 点在经过
点在经过![]() 秒后所在的位置为:
秒后所在的位置为:![]() ,
,
![]() 点在经过
点在经过![]() 秒后所在的位置为:
秒后所在的位置为:![]() ,
,
而此时![]() 和
和![]() 在
在![]() 点相遇,所以
点相遇,所以![]() ,即可求出
,即可求出![]() 的值和点
的值和点![]() 所表示的数;
所表示的数;
②可以假设点![]() 运动
运动![]() 秒后两点之间的距离为5个单位长度,点
秒后两点之间的距离为5个单位长度,点![]() 运动
运动![]() 秒时所在的位置为
秒时所在的位置为![]() ,此时
,此时![]() 点所在的位置为
点所在的位置为![]() ,根据数轴上两点间的距离公式可以列出
,根据数轴上两点间的距离公式可以列出![]() ,即可求出时间
,即可求出时间![]() ;
;
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
∵多项式![]() 是五次四项式,
是五次四项式,
∴![]() ,
,![]() ,
,
∴![]() .
.
故答案为:-3;27;-6.
(2)①解:当运动时间为![]() 秒时,点
秒时,点![]() 所表示的数是
所表示的数是![]() ,点
,点![]() 所表示的数是
所表示的数是![]() ,根据题意得:
,根据题意得:![]() ,
,
解得:![]() ,
,
∴![]() .
.
答:![]() 的值为3,点
的值为3,点![]() 所表示的数是6.
所表示的数是6.
②当运动时间为![]() 秒时(
秒时(![]() ),点
),点![]() 所表示的数是
所表示的数是![]() ,点
,点![]() 所表示的数是
所表示的数是![]() ,
,
根据题意得:![]() ,
,
解得:![]() ,
,![]() .
.
答:点![]() 运动3.5秒或4.5秒后两点之间的距离为5个单位长度.
运动3.5秒或4.5秒后两点之间的距离为5个单位长度.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为( )
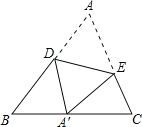
A. 35°B. 40°C. 45°D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2;(填“>”或“<”或“=”)
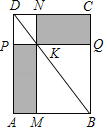
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点![]() 在数轴上分别对应的数为
在数轴上分别对应的数为![]() ,则
,则![]() 两点间的距离表示为
两点间的距离表示为![]() .
.
![]()
根据以上知识解题:
(1)若数轴上两点![]() 表示的数分别为
表示的数分别为![]() ,
,
①当![]() 时,
时,![]() 之间的距离为 ;
之间的距离为 ;
②![]() 之间的距离可用含
之间的距离可用含![]() 的式子表示为
的式子表示为![]() ;
;
③若该两点之间的距离为2,那么![]() 值为 .
值为 .
(2)![]() 的最小值为 ,此时
的最小值为 ,此时![]() 的取值范围是 ;
的取值范围是 ;
(3)若![]() ,则
,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A,B,C为圆心,以![]() AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是________.
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O为等腰三角形ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.
求证:(1)∠AOE=∠BOD;
(2)![]() .
.
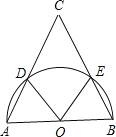
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠后得到
折叠后得到![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .(1)若点
.(1)若点![]() 恰好落在
恰好落在![]() 边上,则
边上,则![]() ______,(2)延长
______,(2)延长![]() 交直线
交直线![]() 于点
于点![]() ,已知
,已知![]() ,则
,则![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com