
【题目】温润有度,为爱加温.近年来设计精巧、物美价廉的暖风机逐渐成为人们冬天必备的“取暖神器”,今年11月下旬某商场计划购进![]() 、
、![]() 两种型号的暖风机共900台,每台
两种型号的暖风机共900台,每台![]() 型号暖风机售价为600元,每台
型号暖风机售价为600元,每台![]() 型号暖风机售价为900元.
型号暖风机售价为900元.
(1)若要使得![]() 、
、![]() 两种型号暖风机的销售额不低于69万元,则至多购进多少台
两种型号暖风机的销售额不低于69万元,则至多购进多少台![]() 型号暖风机?
型号暖风机?
(2)由于质量超群、品质卓越,11月下旬购进的![]() 、
、![]() 两种型号的暖风机全部售完.该商场在12上旬又购进了
两种型号的暖风机全部售完.该商场在12上旬又购进了![]() 、
、![]() 两种型号的暖风机若干台,并且进行“双12”促销活动,每台
两种型号的暖风机若干台,并且进行“双12”促销活动,每台![]() 型号暖风机的售价比其11月下旬的售价优惠
型号暖风机的售价比其11月下旬的售价优惠![]() ,
,![]() 型号暖风机12月上旬的销售量比其在(1)问条件下的最高购进量增加
型号暖风机12月上旬的销售量比其在(1)问条件下的最高购进量增加![]() ,每台
,每台![]() 型号暖风机的售价比其11月下旬的售价优惠
型号暖风机的售价比其11月下旬的售价优惠![]() ,
,![]() 型号暖风机12月上旬的销售量比其在(1)问条件下的最低购进量增加
型号暖风机12月上旬的销售量比其在(1)问条件下的最低购进量增加![]() ,
,![]() 、
、![]() 两种型号的暖风机在12月上旬的销售额比(1)问中最低销售额增加了
两种型号的暖风机在12月上旬的销售额比(1)问中最低销售额增加了![]() ,求
,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
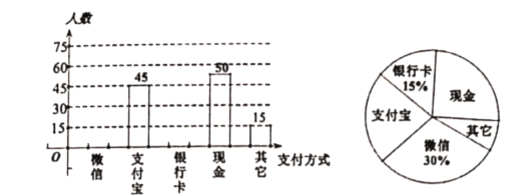
(1)这次活动共调查了多少人;
(2)将条形统计图补充完整;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).

查看答案和解析>>
科目:初中数学 来源: 题型:
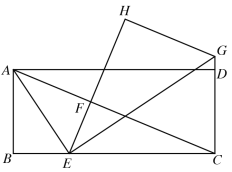
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是对角线,点
是对角线,点![]() 在线段
在线段![]() 上,连结
上,连结![]() ,将
,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 上,点
上,点![]() 在射线
在射线![]() 上,连接
上,连接![]() ,将
,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 所在直线,则线段
所在直线,则线段![]() 的长度为( )
的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
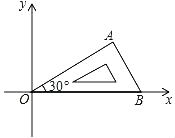
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中,OB 在 x轴上,若 OA=2,将三角板绕原点 O 顺时针旋转 75°,则点 A 的对应点 A′ 的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,点E在弦AB所对的优弧上,且![]() 为半圆,C是
为半圆,C是![]() 上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
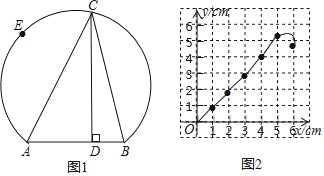
小明根据学习函数的经验,分别对函数y1、y2岁自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 0.78 | 1.76 | 2.85 | 3.98 | 4.95 | 4.47 |
y2/cm | 4 | 4.69 | 5.26 | 5.96 | 5.94 | 4.47 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:
①连接BE,则BE的长约为 cm.
②当以A、B、C为顶点组成的三角形是直角三角形时,BCspan>的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
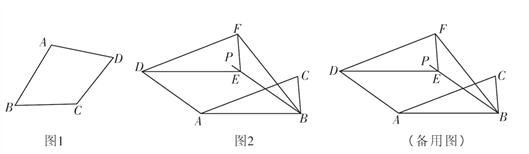
【题目】定义:有一组邻边相等的凸四边形叫做“准菱形”.利用该定义完成以下各题:
(1) 理解
填空:如图1,在四边形ABCD中,若 (填一种情况),则四边形ABCD是“准菱形”;
(2)应用
证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)
(3) 拓展
如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
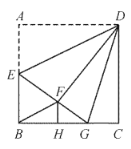
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() .结论:①
.结论:①![]() ;②
;②![]() ≌
≌![]() ;③
;③![]() ∽
∽![]() ;④
;④![]() ;⑤
;⑤![]() .其中的正确的个数是( )
.其中的正确的个数是( )
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com