
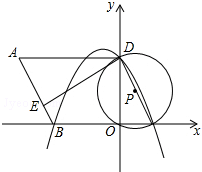
 ��ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ƽ���ı���ABCD�ı�BC��x���ϣ�D����y���ϣ�C������Ϊ��2��0����BC=6����BCD=60�㣬��E��AB��һ�㣬AE=3EB����P��D��O��C���㣬������y=ax2+bx+c����D��B��C���㣮
��ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ƽ���ı���ABCD�ı�BC��x���ϣ�D����y���ϣ�C������Ϊ��2��0����BC=6����BCD=60�㣬��E��AB��һ�㣬AE=3EB����P��D��O��C���㣬������y=ax2+bx+c����D��B��C���㣮���� ��1�������������B�����꣬��ֱ�����������D�����꣬Ȼ����ݴ���ϵ����������ã�
��2������ƽ���ı��ε����ʺ�ֱ�������ε��������AB=4������AE=3EB���AE=3����֤�á�AED�ס�COD���ó���ADE=��CDO���ɡ�ADE+��ODE=90��ó���CDO+��ODE=90������֤�ý��ۣ�
��3���������߽���ʽ���ɶ���ʽ����ö���M�����꣬Ȼ����B��D�����꼴����ã�
��� ��1���⣺��C��2��0����BC=6��
��B��-4��0����
��Rt��OCD����tan��OCD=$\frac{OD}{OC}$��
��OD=2tan60��=2$\sqrt{3}$��
��D��0��2$\sqrt{3}$����
�������ߵĽ���ʽΪy=a��x+4����x-2����
��D��0��2$\sqrt{3}$�������a•4•��-2��=2$\sqrt{3}$�����a=-$\frac{\sqrt{3}}{4}$��
�������ߵĽ���ʽΪy=-$\frac{\sqrt{3}}{4}$��x+4����x-2��=-$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$��
��2��֤������Rt��OCD�У�CD=2OC=4��
���ı���ABCDΪƽ���ı��Σ�
��AB=CD=4��AB��CD����A=��BCD=60�㣬AD=BC=6��
��AE=3BE��
��AE=3��
��$\frac{AE}{AD}$=$\frac{1}{2}$��
��sin��BCD=$\frac{OC}{CD}$=$\frac{1}{2}$��
��$\frac{AE}{AD}$=$\frac{OC}{CD}$��
���ı���ABCD��ƽ���ı��Σ�
���DAE=��DCB=60�㣬
���AED�ס�COD��
���ADE=��CDO��
����ADE+��ODE=90��
���CDO+��ODE=90�㣬
��CD��DE��
�ߡ�DOC=90�㣬
��CDΪ��P��ֱ����
��ED�ǡ�P�����ߣ�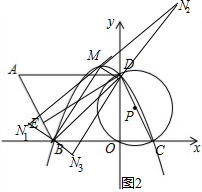
��3���⣺���ڣ�
��y=-$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$=-$\frac{\sqrt{3}}{4}$��x+1��2+$\frac{9\sqrt{3}}{4}$
��M��-1��$\frac{9\sqrt{3}}{4}$����
��B��-4��0����D��0��2$\sqrt{3}$������ͼ2��
��BMΪƽ���ı���BDMN�ĶԽ���ʱ����D����ƽ��4����λ��������ƽ��2$\sqrt{3}$����λ�õ���B��
���M��-1��$\frac{9\sqrt{3}}{4}$������ƽ��4����λ��������ƽ��2$\sqrt{3}$����λ�õ���N1��-5��$\frac{\sqrt{3}}{4}$����
��DMΪƽ���ı���BDMN�ĶԽ���ʱ����B����ƽ��3����λ��
������ƽ��$\frac{9\sqrt{3}}{4}$����λ�õ���M�����D��0��2$\sqrt{3}$������ƽ��3����λ��������ƽ��$\frac{9\sqrt{3}}{4}$����λ�õ���N2��3��$\frac{17\sqrt{3}}{4}$����
��BDΪƽ���ı���BDMN�ĶԽ���ʱ����M����ƽ��3����λ��
������ƽ��$\frac{9\sqrt{3}}{4}$����λ�õ���B�����D��0��2$\sqrt{3}$������ƽ��3����λ��������ƽ��$\frac{9\sqrt{3}}{4}$����λ�õ���N3��-3��-$\frac{\sqrt{3}}{4}$����
������������N��������-5��$\frac{\sqrt{3}}{4}$������3��$\frac{17\sqrt{3}}{4}$������-3��-$\frac{\sqrt{3}}{4}$����
���� �����˶��κ����ۺ��⣺���������ô���ϵ��������κ�������ʽ�����κ��������ʺ����������ε��ж������ʣ�����ƽ���ı��ε����ʵ�ƽ�ƵĹ��ɣ���֤��Բ�����ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
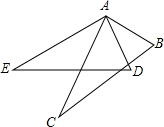 ��ͼ����֪��BAC=��DAE=90�㣬AB=AD��Ҫʹ��ABC�ա�ADE������Ҫ���ӵ�������AE=AC��ֻ������һ���������ɣ�
��ͼ����֪��BAC=��DAE=90�㣬AB=AD��Ҫʹ��ABC�ա�ADE������Ҫ���ӵ�������AE=AC��ֻ������һ���������ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
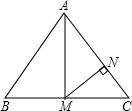 ��ͼ�ڡ�ABC�У�AB=AC=10��BC=12����MΪBC���е㣬MN��AC�ڵ�N����MN���ڣ�������
��ͼ�ڡ�ABC�У�AB=AC=10��BC=12����MΪBC���е㣬MN��AC�ڵ�N����MN���ڣ�������| A�� | $\frac{12}{5}$ | B�� | $\frac{18}{5}$ | C�� | $\frac{24}{5}$ | D�� | $\frac{32}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���εĶԽ�����ƽ�� | B�� | �����εĶԽ����ഹֱƽ�� | ||
| C�� | ���εĶԽ��������ƽ�� | D�� | ƽ���ı��εĶԽ�������Ҵ�ֱ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
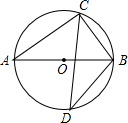 ��ͼ��ʾ���ڡ�O�У�ABΪ��O��ֱ����AC=8��sinD=$\frac{3}{5}$����BC=6��
��ͼ��ʾ���ڡ�O�У�ABΪ��O��ֱ����AC=8��sinD=$\frac{3}{5}$����BC=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�Ƕ��κ���y=ax2+bx+c��a��0����ͼ���������жϣ���2a+b=0���ڵ�-1��x��3ʱ��y��0��������x1��y1������x2��y2���ں���ͼ���ϣ���x1��x2ʱ��y1��y2����9a+3b+c=0��������ȷ���ǣ�������
��ͼ�Ƕ��κ���y=ax2+bx+c��a��0����ͼ���������жϣ���2a+b=0���ڵ�-1��x��3ʱ��y��0��������x1��y1������x2��y2���ں���ͼ���ϣ���x1��x2ʱ��y1��y2����9a+3b+c=0��������ȷ���ǣ�������| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �٢ۢ� | D�� | �ڢۢ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com