
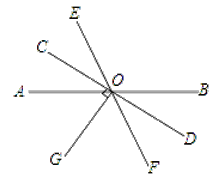
【题目】如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
【答案】(1)∠AOG=54o;(2)OC是∠AOE的平分线,理由见解析.
【解析】
(1)根据对顶角的性质可得∠AOC=∠BOD=36°,利用垂直定义可得∠COG=90°,再计算出∠AOG的度数即可;(2)根据角平分线定义以及垂直定义可得∠COA=∠DOF,再根据对顶角相等可得∠DOF=∠COE,进而得出∠AOC=∠COE,即可得到OC平分∠AOE.
解:(1)∵AB、CD相交于点O,
∴∠AOC=∠BOD=36°,
∵OG⊥CD,
∴∠COG=90°,
即∠AOC+∠AOG=90°,
∴∠AOG=90°﹣∠AOC=90°﹣36o=54o;
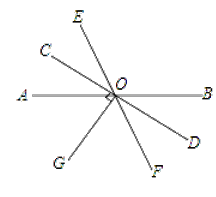
(2)OC是∠AOE的平分线.
∵OG是∠AOF的角平分线,
∴∠AOG=∠GOF,
∵OG⊥CD,
∴∠COG=∠DOG=90°,
∴∠COA=∠DOF,
又∵∠DOF=∠COE,
∴∠AOC=∠COE,
∴OC平分∠AOE.


科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )
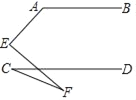
A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
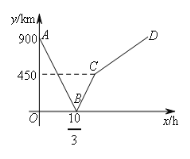
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,各自到达终点后停止行驶。设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,则两车相遇之后又经过___________小时,两车相距720km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy,直线y=x﹣1与y轴交于点A,与双曲线y= ![]() 交于点B(m,2).
交于点B(m,2).
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若△ABC的面积为6,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
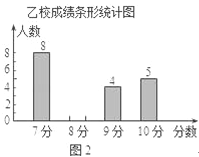
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
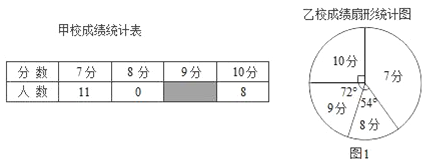
(1)在图1中,“7分”所在扇形的圆心角等于 °.
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点![]() 按如图方式叠放在一起,当
按如图方式叠放在一起,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示:![]() ,
,![]() ,
,![]() .
.

(1)①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出![]() 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“数学兴趣小组”根据学习函数的经验,对函数y= ![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整: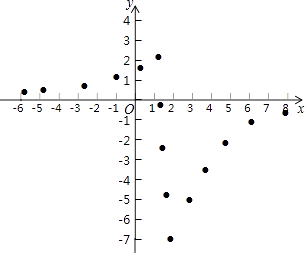
(1)该函数的自变量x的取值范围是;
(2)同学们先找到y与x的几组对应值,然后在下图的平面直角坐标系xOy中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
(3)结合画出的函数图象,写出该函数的一条性质: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com