
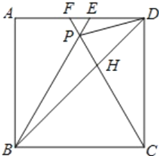
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论,其中正确结论的个数是( )
①△BDE∽△DPE;②![]() ;③
;③![]() ;④tan∠DBE=
;④tan∠DBE=![]() .
.
A.4个B.3个C.2个D.1个
【答案】B
【解析】
根据等边三角形的性质和正方形的性质,得到∠PCD=30°,于是得到∠CPD=∠CDP=75°,证得∠EDP=∠PBD=15°,于是得到△BDE∽△DPE,故①正确由于∠FDP=∠PBD,∠DFP=∠BPC=60°,推出△DFP∽△BPH,得到![]() 故②错误;由于∠PDH=∠PCD=30°,∠DPH=∠DPC,推出△DPH∽△CPD,得到
故②错误;由于∠PDH=∠PCD=30°,∠DPH=∠DPC,推出△DPH∽△CPD,得到![]() ,PB=CD,等量代换得到PD2=PHPB,故③正确;过P作PM⊥CD,PN⊥BC,设正方形ABCD的边长是4,△BPC为正三角形,于是得到∠PBC=∠PCB=60°,PB=PC=BC=CD=4,求得∠PCD=30°,根据三角函数的定义得到CM=PN=PBsin60°=4×
,PB=CD,等量代换得到PD2=PHPB,故③正确;过P作PM⊥CD,PN⊥BC,设正方形ABCD的边长是4,△BPC为正三角形,于是得到∠PBC=∠PCB=60°,PB=PC=BC=CD=4,求得∠PCD=30°,根据三角函数的定义得到CM=PN=PBsin60°=4×![]() ,PM=PCsin30°=2,由平行线的性质得到∠EDP=∠DPM,等量代换得到∠DBE=∠DPM,于是求得tan∠DBE=tan∠DPM=
,PM=PCsin30°=2,由平行线的性质得到∠EDP=∠DPM,等量代换得到∠DBE=∠DPM,于是求得tan∠DBE=tan∠DPM=![]() ,故④正确.
,故④正确.
∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
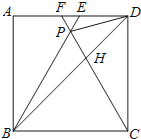
∴∠CPD=∠CDP=75°,∴∠PDE=15°,
∵∠PBD=∠PBC-∠HBC=60°-45°=15°,
∴∠EBD=∠EDP,
∵∠DEP=∠DEB,
∴△BDE∽△DPE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH,
∴![]() ,故②错误;
,故②错误;
∵∠PDH=∠PCD=30°,
∵∠DPH=∠DPC,
∴△DPH∽△CDP,
∴![]() ,
,
∴PD2=PHCD,
∵PB=CD,
∴PD2=PHPB,故③正确;
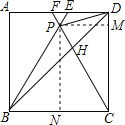
如图,过P作PM⊥CD,PN⊥BC,
设正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
∴CM=PN=PBsin60°=4×![]() ,PM=PCsin30°=2,
,PM=PCsin30°=2,
∵DE∥PM,
∴∠EDP=∠DPM,
∴∠DBE=∠DPM,
∴tan∠DBE=tan∠DPM=![]() ,故④正确;
,故④正确;
故选:B.


科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC=____________度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假期,黔西南州某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图所示是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
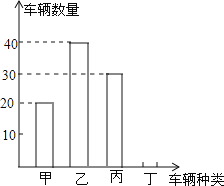
(1)若去丁地的车票占全部车票的10%,请求出去丁地的车票数量,并补全统计图(如图所示).
(2)若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张(所有车票的形状、大小、质地完全相同、均匀),那么员工小胡抽到去甲地的车票的概率是多少?
(3)若有一张车票,小王和小李都想去,决定采取摸球的方式确定,具体规则:“每人从不透明袋子中摸出分别标有1、2、3、4的四个球中摸出一球(球除数字不同外完全相同),并放回让另一人摸,若小王摸得的数字比小李的小,车票给小王,否则给小李.”试用列表法或画树状图的方法分析这个规则对双方是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定关于x的二次函数y=kx2﹣4kx+3(k≠0),
(1)当该二次函数与x轴只有一个公共点时,求k的值;
(2)当该二次函数与x轴有2个公共点时,设这两个公共点为A、B,已知AB=2,求k的值;
(3)由于k的变化,该二次函数的图象性质也随之变化,但也有不会变化的性质,某数学学习小组在探究时得出以下结论:
①与y轴的交点不变;②对称轴不变;③一定经过两个定点;
请判断以上结论是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB过x轴上的点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
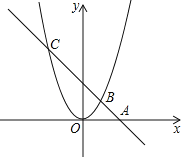
(1)求直线AB和抛物线的函数关系式;
(2)在抛物线上是否存在一点D,使得S△OAD=S△OBC?若不存在,请说明理由;若存在,请求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P, AC=PC,∠COB=2∠PCB.
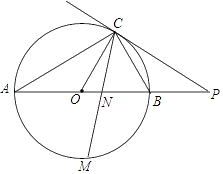
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的标价为600元/件,经过两次降价后的价格为486元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为460元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3788元.问第一次降价后至少要售出该种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
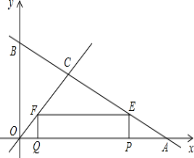
(1)求点P运动的速度是多少?
(2)当t为多少秒时,矩形PEFQ为正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)与x轴相交于A、B两点,与y轴的交于点C(0,﹣3).
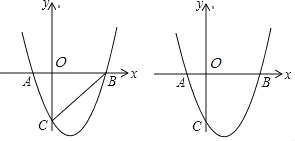
(1)求抛物线的解析式的一般式.
(2)若抛物线上有一点P,满足∠ACO=∠PCB,求P点坐标.
(3)直线l:y=kx﹣k+2与抛物线交于E、F两点,当点B到直线l的距离最大时,求△BEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com