已知：关于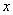
的一元二次方程
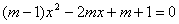（m>1）．
（1）求证：方程总有两个不相等的实数根.
（2）
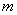为何整数时，此方程的两个实数根都为正整数？
科目：初中数学 来源： 题型：
阅读下面材料：
如果一个三角形和一个平行四边形满足条件：三角形的一边与平行四边形的一边重合，三角形这边所对的顶点在平行四边形这边的
对边上，则称这样的平行四边形为三角形的“友好平行四边形”．如图1 所示，平行四边形
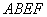即为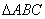
的“友好平行四边形”．
请解决下列问题:
（1）仿照以上叙述,说明什么是一个三角形的“友好矩形”；
（2）若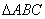是钝角三角形，则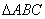显然只有一个“友好矩形”，
若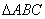是直角三角形，其“友好矩形”有 个；
（3）若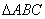是锐角三角形，且
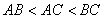，如图2，请画出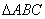的所有“友好矩形”；指出其中周长最小的“友好矩形”并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
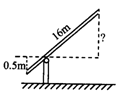
如图，铁路道口的栏杆短臂长1m，长臂长16m．当短臂端点下降0.5m时，长臂端点升高（杆的宽度忽略不计）．
A．4m B．6m C．8m D．12m
查看答案和解析>>
科目：初中数学 来源： 题型：
在平面直角坐标系xOy中，二次函数y=2x2+bx+c的图象经过（-1，0）和（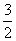
，0）两点.
（1）求此二次函数的表达式.
（2）直接写出当-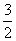＜x＜1时，y的取值范围.
（3）将一次函数 y=(1-m)x+2的图象向下
平移m个单位后，与二次函数y=2x2+bx+c图象交点的横坐标分别是a和b,其中a<2<b，试求m的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
阅读下面资料：
小明遇到这样一个问题：如图1，对面积为a的△ABC逐次进行以下操作：分别延长AB、
BC、CA至A1、B1、C1，使得A1B=AB，B1C=BC，C1A=CA，顺次连接A1、B1、C1，
得到△A1B1C1，记其面积为S1，求S1的值．
小明是这样思考和解决这个问题的：如图2，连接A1C、B1A、C1B，因为A1B=AB，
B1C=BC，C1A=CA，根据等高两三角形的面积比等于底之比，
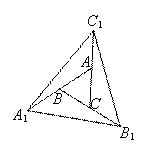
图1 图2
所以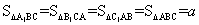
，由此继续推理，从而解决了这个问题．
（1）请直接写出S1= ；（用含字母a的式子表示）．
请参考小明同学思考问题的方法，解决下列问题：
（2）如图3，对面积为a的△ABC逐次进行以下操作：分别延长AB、BC、CA至A1、
B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其
面积为S2，求S2的值．
（3）如图4，P为△ABC内一点，连接AP、BP、CP并延长分别交边BC、AC、AB于
点D、E、F，则把△ABC分成六个小三角形，其中四个小三角形面积已在图上标明，设△APE的面积为y，△BPF的面积为x，
①求△APE ，△BPF，△APF 面积之间的关系；
②求△ABC的面积．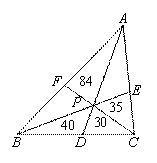
|
| ||||
查看答案和解析>>
科目：初中数学 来源： 题型：
某科研机构对我区400户有两个孩子的家庭进行了调查，得到了表格中的数据，其中(男，女)代表第一个孩子是男孩，第二个孩子是女孩，其余类推．由数据，请估计我区两个孩子家庭中男孩与女孩的人数比为 ： ．
| 类别 | 数量（户） |
| (男，男) | 101 |
| (男，女) | 99 |
| (女，男) | 116 |
| (女，女) | 84 |
| 合计 | 400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．
