
【题目】如图,点A(a,1)、B(﹣1,b)都在函数![]() (x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .
(x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .

【答案】y=x+2
【解析】
试题分析:作点A关于x轴的对称点A′,作点B关于y轴的对称点B′,连接A′B′,分别于x、y轴交于点P、Q点,此时四边形PABQ的周长最小,由点A、B均为反比例函数上的点,由此即可求出a、b值,即得出点A、B的坐标,再根据对称的性质找出点A′、B′的坐标,结合两点的坐标利用待定系数法即可求出PQ所在直线的解析式.
解:作点A关于x轴的对称点A′,作点B关于y轴的对称点B′,连接A′B′,分别于x、y轴交于点P、Q点,此时四边形PABQ的周长最小,如图所示.
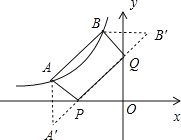
∵点A(a,1)、B(﹣1,b)都在函数![]() (x<0)的图象上,
(x<0)的图象上,
∴a=﹣3÷1=﹣3,b=﹣3÷(﹣1)=3,
∴点A(﹣3,1),点B(﹣1,3),
∴点A′(﹣3,﹣1),点B′(1,3).
设直线A′B′的解析式为y=kx+c,
∴![]() ,解得:
,解得:![]() ,
,
∴直线A′B′的解析式为y=x+2,即PQ所在直线的解析式是y=x+2.
故答案为:y=x+2.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,P是直线CD上的一个动点,(点P不与F重合)
(1)当点P在射线FC上移动时,∠FMP+∠FPM =∠AEF成立吗?请说明理由。
(2)当点P在射线FD上移动时,∠FMP+∠FPM与∠AEF有什么关系?并说明你的理由


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于抛物线y=(x-1)2-2,下列说法中错误的是( )
A.顶点坐标为(1,-2)
B.对称轴是直线x=1
C.当x>1时,y随x的增大而减小
D.开口方向向上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】廉贻中学为每个学生编号,设定末尾用1表示男生,用2表示女生。如果152132表示“2015年入学的2班13号的同学,是位女生”,那么今年入学的3班19号男生的编号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋大米的标准重量为15kg.把一袋重15.5kg的大米记为+0.5kg,则一袋重14.8kg的大米记为( )
A. -14.8kg B. +14.8kg C. -0.2kg D. 0.2kg
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长都为1个单位长度, △ABC的三个顶点的位置如图所示,现将△ABC平移后得△EDF,使点B的对应点为点D,点A对应点为点E.

(1)画出△EDF;
(2)线段BD与AE有何位置关系与数量关系? .
(3)连接CD、BD,则四边形ABDC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解题过程,并在横线上补全推理过程或依据.
已知:如图, DE∥BC,DF、BE分别平分∠ADE、∠ABC.试说明∠FDE=∠DEB.
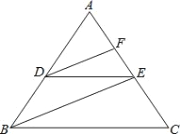
解:∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC (已知)
∴∠ADF=![]() ∠ADE
∠ADE
∠ABE=![]() ∠ABC(角平分线定义)
∠ABC(角平分线定义)
∴∠ADF=∠ABE( )
∴DF∥ .( )
∴∠FDE=∠DEB.( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com