
����Ŀ���Ķ����ϣ���������![]() ��
��![]() ���Ե�����֮��ľ��룺
���Ե�����֮��ľ��룺![]() ��
��
��������![]() ��
��![]() ���Ե�����֮��ľ��룺
���Ե�����֮��ľ��룺![]() ��
��
��������![]() ��
��![]() ���Ե�����֮��ľ��룺
���Ե�����֮��ľ��룺![]() ��
��
�������ϵ�![]() ��
��![]() �ֱ��ʾ��
�ֱ��ʾ��![]() ��
��![]() ����
����![]() ��
��![]() ����֮��ľ���
����֮��ľ���![]() ��
��
��ش��������⣺
��![]() �������ϱ�ʾ
�������ϱ�ʾ![]() ��
��![]() ������֮��ľ�����__________��
������֮��ľ�����__________��
�����ϱ�ʾ��![]() ��
��![]() ������֮��ľ����ʾΪ__________�������ϱ�ʾ��__________��__________������֮��ľ����ʾΪ
������֮��ľ����ʾΪ__________�������ϱ�ʾ��__________��__________������֮��ľ����ʾΪ![]() ��
��
��![]() �����꼶�о���ѧϰС������ѧ��ʦָ���£���ʽ�ӽ���̽����
�����꼶�о���ѧϰС������ѧ��ʦָ���£���ʽ�ӽ���̽����![]() ��
��
�������ڲݸ�ֽ�ϻ������ᣬ����ʾ��![]() �ĵ���
�ĵ���![]() ��
��![]() ֮���ƶ�ʱ��
֮���ƶ�ʱ��![]() ��ֵ����һ���̶���ֵΪ��__________����ֱ��д�������
��ֵ����һ���̶���ֵΪ��__________����ֱ��д�������
�������ڲݸ�ֽ�ϻ������ᣬҪʹ![]() �����������������ĵ��ʾ�������ǣ�__________��ֱ��д���������
�����������������ĵ��ʾ�������ǣ�__________��ֱ��д���������
���𰸡���1��3��|x3|��x��-2����2����5����5��-4.
��������
��1�����������ҳ�������������ľ���ļ��㹫ʽ��Ȼ����м��㼴�ɣ�
��2���ٸ���x��ȡֵ��Χ���������ֵ���ɣ�
�ڷ�Ϊx��3��x��2����������ۣ�
�⣺��1�������ϱ�ʾ2��5������֮��ľ��룽|2��5��|��3��
�����ϱ�ʾ��![]() ��
��![]() ������֮��ľ����ʾΪ��|x3|��
������֮��ľ����ʾΪ��|x3|��
�����ϱ�ʾ��x��2������֮��ľ����ʾΪ|x��2|��
��2���ٵ�2��x��3ʱ��![]() ��3x��x��2��5��
��3x��x��2��5��
�ڵ�x��3ʱ��![]() =x3��x��2��9��
=x3��x��2��9��
��ã�x��5��
��x��2ʱ��![]() =3xx2��9��
=3xx2��9��
���x��4��
��x��5��x��-4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
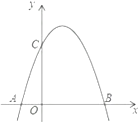
����Ŀ����ͼ���ǽ�������y=-x2 ƽ�ƺ�õ��������ߣ���Գ���Ϊx=1����x���һ������ΪA(-1,0) ����һ����ΪB����y�ύ��ΪC��
��1���������ߵĺ�������ʽ��
��2������N Ϊ��������һ�㣬��BC��NC�����N�����ꣻ
��3����P����������һ�㣬��Q��һ�κ���y=![]() x+
x+![]() ��ͼ����һ�㣬���ı���OAPQΪƽ���ı��Σ������ĵ�P��Q�Ƿ���ڣ������ڣ��ֱ������P��Q�����꣬�������ڣ�˵�����ɣ�
��ͼ����һ�㣬���ı���OAPQΪƽ���ı��Σ������ĵ�P��Q�Ƿ���ڣ������ڣ��ֱ������P��Q�����꣬�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��OCƽ�֡�AOB,��P������OC�ϵ�һ��.
��OCƽ�֡�AOB,��P������OC�ϵ�һ��.

��1����ͼһ������P��PD��OA��PE��OB��˵��PD��PE��ȵ�����.
��2����ͼ���������F��G�ֱ�������OA��OB�ϣ��ҡ�FPG=60�㣬��ô�߶�PF��PG�������˵�����ɣ�
��3���ڣ�2���������£�����FG,![]() ��ʲô��״�������Σ���˵������.
��ʲô��״�������Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��̽������д������������ͼ�ۼ������� 0.5 ����ɫǩ�ֱ�����ۼ��� ��ͼ����DBC �͡�ECB ����ABC �����������
(1)��ֱ�ߺ�Բ��ֱ�����DBC �͡�ECB ��ƽ���ߣ��������ཻ�ڵ� P��
(2)���� P �ֱ�ֱ�� AB��AC��BC �Ĵ��߶� PM��PN��PQ������ Ϊ M��N��Q��
(3) PM��PN��PQ ����𣿣�ֱ��д�����ۣ�����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ˮ������ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ����������Ƕ��ٽ�ú�x�Ĵ���ʽ��ʾ����
��2����������ˮ��Ҫ��ÿ��ӯ��300Ԫ���ұ�֤ÿ�������۳�260���ôˮ�����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС����̽��������ȫ��ʱ���������������ֵ��͵Ļ���ͼ�Σ�
![]() ��ͼ1����֪����
��ͼ1����֪����![]() �У�
��![]() ��
��![]() ��ֱ��m������A��
��ֱ��m������A��![]() ֱ��m��
ֱ��m��![]() ֱ��m������ֱ�Ϊ��D��
ֱ��m������ֱ�Ϊ��D��![]() �Բ���DE��BD��CE��������������ϵ����ֱ��д����
�Բ���DE��BD��CE��������������ϵ����ֱ��д����
![]() ��ԱСӱ�룬��������Dz���ֱ�ǣ��ǽ����Ƿ������أ���ͼ2����
��ԱСӱ�룬��������Dz���ֱ�ǣ��ǽ����Ƿ������أ���ͼ2����![]() �е�������Ϊ����
�е�������Ϊ����![]() �У�
�У�![]() ��D��A��E���㶼��ֱ��m�ϣ�������
��D��A��E���㶼��ֱ��m�ϣ�������![]() ����
����![]() Ϊ������ǻ�۽�
Ϊ������ǻ�۽�![]() ����������������֤����������������˵�����ɣ�
����������������֤����������������˵�����ɣ�
![]() ��ѧ��ʦ���������ǵ�̽���������������������֪ʶ��������⣺
��ѧ��ʦ���������ǵ�̽���������������������֪ʶ��������⣺
��ͼ3��F��![]() ��ƽ�����ϵ�һ�㣬��
��ƽ�����ϵ�һ�㣬��![]() ��
��![]() ��Ϊ�ȱ������Σ�D��E�ֱ���ֱ��m��A����������Ķ���
��Ϊ�ȱ������Σ�D��E�ֱ���ֱ��m��A����������Ķ���![]() ��E��A�����غ�
��E��A�����غ�![]() �����˶��������߶�DE�ij���ʼ��Ϊn������BD��CE����
�����˶��������߶�DE�ij���ʼ��Ϊn������BD��CE����![]() �����ж�
�����ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������о�װ�����ų�������ֵ����ȫ��ͬ�Ŀ�Ƭ���״��е����ſ�Ƭ�������������ֵΪ��7����1��3���Ҵ��е����ſ�Ƭ���������ֵΪ��2��1��6���ȴӼ״������ȡ��һ�ſ�Ƭ����x��ʾȡ���Ŀ�Ƭ�ϵ���ֵ���ٴ��Ҵ������ȡ��һ�ſ�Ƭ����y��ʾȡ���Ŀ�Ƭ�ϵ���ֵ����x��y�ֱ���Ϊ��A�ĺ��������������
��1�����ʵ��ķ���д����A��x��y�������������
��2�����A���ڷ���������![]() ͼ���ϵĸ�����
ͼ���ϵĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
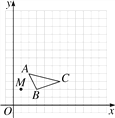
����Ŀ����13��13������ͼ�У���֪��ABC�͵�M(1��2)��
(1)�Ե�MΪλ�����ģ�������ABC��λ��ͼ����A��B��C����������A��B��C������ABC��λ�Ʊ�Ϊ2��
(2)д����A��B��C���ĸ��������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=��x2+2x+m��
��1��������κ�����ͼ����x�����������㣬��m��ȡֵ��Χ��
��2����ͼ�����κ�����ͼ�����A��3��0������y�ύ�ڵ�B��ֱ��AB��������κ���ͼ��ĶԳ��ύ�ڵ�P�����P�����꣮
��3������ͼ��ֱ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com