

分析 作MD∥BC,交AB于D,易证△DMP≌△BNP;
(1)根据△DMP≌△BNP即可求得$\frac{PM}{PN}$和$\frac{AP}{BP}$的值;
(2)取n=2,即可求得$\frac{BP}{AP}$=$\frac{1}{2}$,即可解题;
(3)当PA=5PB时,可求得$\frac{AM}{CM}$=$\frac{AD}{BD}$=2,即可解题.
解答 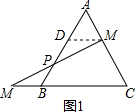 解:如图1,作MD∥BC,交AB于D,
解:如图1,作MD∥BC,交AB于D,
则AM=DM=AD,
∴△ADM∽△ABC,
又∵AM=BN,
∴BN=DM,
在△DMP和△BNP中,
$\left\{\begin{array}{l}{∠DPM=∠BPN}\\{DM=BN}\\{∠MDP=∠NBP}\end{array}\right.$,
∴△DMP≌△BNP(ASA),
∴PM=PN,PD=PB,
∴$\frac{PM}{PN}$=1,
(1)当n=1时(即点M是AC中点),AM=DM=BN,
∴PB=$\frac{1}{2}$BD,
又∵AD=BD=$\frac{1}{2}$AB,
∴$\frac{AB}{BP}$=4,
∴$\frac{AP}{BP}$=3,
(2)当n=2时,$\frac{AD}{AB}$=$\frac{AM}{AC}$=$\frac{1}{3}$,$\frac{BD}{AB}$=$\frac{2}{3}$,$\frac{BP}{AB}$=$\frac{1}{3}$,
∴$\frac{BP}{AP}$=$\frac{1}{2}$,
即AP=2PB;
(3)当PA=5PB时,$\frac{PB}{AB}$=$\frac{1}{6}$,$\frac{BD}{AB}$=$\frac{1}{3}$,$\frac{AM}{MC}$=$\frac{AD}{BD}$=2,
∴n=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了全等三角形的判定,考查了相似三角形的判定,考查了全等三角形对应边相等的性质,考查了相似三角形对应边比例相等的性质.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
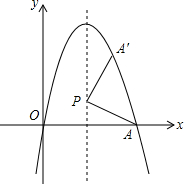 如图,经过原点的抛物线y=-x2+6x与x轴的另一个交点为A.
如图,经过原点的抛物线y=-x2+6x与x轴的另一个交点为A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠A=α,BI、CI分别平分∠ABC,∠ACB,则∠BIC=90°+$\frac{α}{2}$,若BM、CM分别为∠ABC,∠ACB的外角平分线,则∠M=90°-$\frac{α}{2}$.
如图,△ABC中,∠A=α,BI、CI分别平分∠ABC,∠ACB,则∠BIC=90°+$\frac{α}{2}$,若BM、CM分别为∠ABC,∠ACB的外角平分线,则∠M=90°-$\frac{α}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
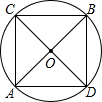 如图所示,AB,CD是⊙O的两条相互垂直的直径.
如图所示,AB,CD是⊙O的两条相互垂直的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,两弦AB与CD的中点分别是P,Q,且$\widehat{AB}$=$\widehat{CD}$,连接PQ.求证:∠APQ=∠CQP.
如图,在⊙O中,两弦AB与CD的中点分别是P,Q,且$\widehat{AB}$=$\widehat{CD}$,连接PQ.求证:∠APQ=∠CQP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com