
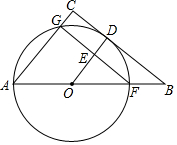
 如图,在△ABC中,F是AB上一点,以AF为直径的⊙O切BC于点D,交AC于点G,AC∥OD,OD与GF交于点E.
如图,在△ABC中,F是AB上一点,以AF为直径的⊙O切BC于点D,交AC于点G,AC∥OD,OD与GF交于点E.分析 (1)根据切线的性质,可得OD⊥BC,利用平行线的性质可证得∠C=90°,由AF为直径,可得∠AGF=90°,进而可得BC∥GF;
(2)先证明四边形CGED为矩形,再根据锐角三角函数、勾股定理求GF,OE,DE的长,进而可求四边形CGED的面积.
解答 证明:(1)∵⊙O切BC于点D,
∴OD⊥BC,
∵AC∥OD,
∴∠C=∠ODB=90°,
∵AF为⊙O直径,
∴∠AGF=90°=∠C,
∴BC∥GF.
解:(2)∵AC∥OD,BC∥GF
∴四边形CGED为平行四边形,
∵∠C=90°,
∴四边形CGED为矩形,
∵tanA=$\frac{4}{3}$,
∴sinA=$\frac{4}{5}$,
∵AF=2AO=2a,OF=a,
∴GF=AF•sinA=2a×$\frac{4}{5}$=$\frac{8a}{5}$,
∵OD⊥BC,
∴GE=EF=$\frac{1}{2}GF$=$\frac{4a}{5}$,
在Rt△OEF中,OE=$\sqrt{O{F}^{2}-E{F}^{2}}$=$\sqrt{{a}^{2}-(\frac{4a}{5})^{2}}$=$\frac{3a}{5}$,
∴DE=OD-OE=a-$\frac{3a}{5}$=$\frac{2a}{5}$,
∴S四边形CGED=GE•DE=$\frac{4a}{5}$×$\frac{2a}{5}$=$\frac{8{a}^{2}}{25}$.
点评 本题主要考查切线的性质,解决此类题目时,要灵活运用切线的性质和平行线的性质与判定.


科目:初中数学 来源: 题型:解答题
 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校组织全校2 000名学生进行了环保知识竞赛.为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整):
某校组织全校2 000名学生进行了环保知识竞赛.为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整):| 分组 | 频数 | 频率 |
| 50.5~60.5 | 20 | 0.05 |
| 60.5~70.5 | 48 | △ |
| 70.5~80.5 | △ | 0.20 |
| 80.5~90.5 | 104 | 0.26 |
| 90.5~100.5 | 148 | △ |
| 合计 | △ | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O是直线AB、CD的交点,OE⊥AB,OF⊥CD,OM是∠BOF的平分线.
如图,点O是直线AB、CD的交点,OE⊥AB,OF⊥CD,OM是∠BOF的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com