
【题目】已知多项式ax5+bx3+3x+c,当x=0时,该代数式的值为﹣1.
(1)求c的值;
(2)已知当x=3时,该式子的值为9,试求当x=﹣3时该式子的值;
(3)在第(2)小题的已知条件下,若有3a=5b成立,试比较a+b与c的大小?
【答案】
(1)解:把x=0代入代数式,得到ax5+bx3+3x+c=c=﹣1;
∴c=﹣1
(2)解: 把x=3代入代数式,得到ax5+bx3+3x+c=35a+33b+3×3+c=9,
∴35a+33b+c=0;35a+33b=﹣c=1,
当x=﹣3时,
原式=(﹣3)5a+(﹣3)3b+3×(﹣3)+c
=﹣(35a+33b)﹣9+c
=c﹣9+c=2c﹣9
=﹣2﹣9
=﹣11
(3)解: 由(2)题得35a+33b=1,即9a+b= ![]() ,
,
又∵3a=5b,所以15b+b= ![]() ,
,
∴b= ![]() >0,
>0,
则a= ![]() b>0,
b>0,
∴a+b>0,
∵c=﹣1<0,
∴a+b>c
【解析】(1)把x=0代入,可得到关于c的方程,可求得c的值;(2)把x=3代入可得到关于a、b的关系式,结合c=﹣1,可求得答案;(3)由(2)的关系式结合条件可求得a+b的符号,结合c=﹣1可比较其大小.


科目:初中数学 来源: 题型:
【题目】给出下列说法:①棱柱的上、下底面的形状相同;②相等的角是对顶角;③若AB=BC,则点B为线段AC的中点;④直线外一点与直线上各点连接的所有线段中,垂线段最短.
其中正确说法的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,已知点A(0,2)、点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
(1)填空:点D的坐标为_________,点E的坐标为_______________.
(2)若抛物线![]() 经过A、D、E三点,求该抛物线的解析式.
经过A、D、E三点,求该抛物线的解析式.
(3)若正方形和抛物线均以每秒![]() 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在![]() 轴上时,正方形和抛物线均停止运动.
轴上时,正方形和抛物线均停止运动.
①在运动过程中,设正方形落在y轴右侧部分的面积为![]() ,求
,求![]() 关于平移时间
关于平移时间![]() (秒)的函数关系式,并写出相应自变量
(秒)的函数关系式,并写出相应自变量![]() 的取值范围.
的取值范围.
②运动停止时,求抛物线的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据等式和不等式的性质,可以得到:若a﹣b>0,则a>b;若a﹣b=0,则a=b;若a﹣b<0,则a<b.这是利用“作差法”比较两个数或两个代数式值的大小.
(1)试比较代数式5m2﹣4m+2与4m2﹣4m﹣7的值之间的大小关系;
(2)已知A=5m2﹣4( ![]() m﹣
m﹣ ![]() ),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,L与M相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为 . 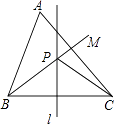
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的AB边上,且∠ACD=∠A. 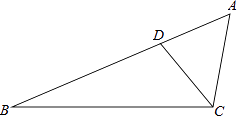
(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C = 90°,AD是∠BAC的平分线,DE⊥AB于E,若DE = 8cm,DB = 10cm则BC等于( )
A.14cm
B.16cm
C.18cm
D.20cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘客轮由西向东行驶,在A点处测得距灯塔B的距离为40nmile,前进方向AC与直线AB夹角为30°.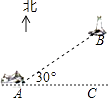
(1)分别用方向和距离描述灯塔相对于客轮的位置和客轮相对于灯塔的位置?
(2)如果在灯塔B的周围25nmile的范围内有暗礁,客轮若不改变方向有没有触礁的危险.(温馨提示:按照适当的比例画图测量换算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com