
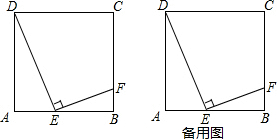
分析 (1)根据两个角对应相等的两个三角形相似证明△ADE∽△BEF;
(2)根据相似三角形的性质得到成比例相等,代入已知数据整理即可得到二次函数的解析式,根据二次函数的性质求出最大值;
(3)根据同弧所对的圆周角相等和锐角三角函数的概念求出DF的长,得到答案.
解答 (1)证明:∵∠DEF=90°,
∴∠AED+∠BEF=90°,又∠AED+∠ADE=90°,
∴∠ADE=∠BEF,又∠A=∠B,
∴△ADE∽△BEF;
(2)解:∵△ADE∽△BEF,
∴$\frac{AD}{BE}$=$\frac{AE}{BF}$,又AE=x,BF=y,AD=4,
∴$\frac{4}{x}$=$\frac{4-x}{y}$,
解得,y=-$\frac{1}{4}$x2+x=-$\frac{1}{4}$(x-2)2+1,
∴当x=2时,y有最大值,最大值为1;
(3)解:∵D、C、F、E四点共圆,
∴∠CEF=∠CDF,
∴sin∠CEF=sin∠CDF=$\frac{CF}{DF}$=$\frac{3}{5}$,又CD=4,
∴DF=5,
∵∠DCF=90°,
∴DF为此圆直径,
∴此圆直径为5.
点评 本题考查的是正方形的性质、相似三角形的判定和性质、二次函数的性质以及四点共圆的知识,掌握相关的性质定理和判定定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\sqrt{7}$ | C. | $\root{2}{{\frac{1}{2}}}$ | D. | $\sqrt{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
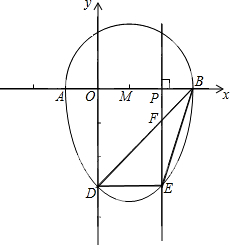 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s,连接PQ、AQ、CP,设点P、Q运动的时间为t s.当t为何值时,四边形ABQP是矩形?
如图所示,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s,连接PQ、AQ、CP,设点P、Q运动的时间为t s.当t为何值时,四边形ABQP是矩形?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com