
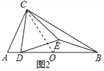
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
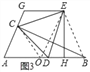
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
【答案】(1)证明见解析;(2)ED=EB,证明见解析;(3)CG=2.
【解析】
试题(1)、根据等边三角形的性质得出∠CED=60°,从而得出∠EDB=30°,从而得出DE=BE;(2)、取AB的中点O,连接CO、EO,根据△ACO和△CDE为等边三角形,从而得出△ACD和△OCE全等,然后得出△COE和△BOE全等,从而得出答案;(3)、取AB的中点O,连接CO、EO、EB,根据题意得出△COE和△BOE全等,然后得出△CEG和△DCO全等,设CG=a,则AG=5a,OD=a,根据题意列出一元一次方程求出a的值得出答案.
试题解析:(1)、证明:∵△CDE是等边三角形, ∴∠CED=60°, ∴∠EDB=60°﹣∠B=30°,
∴∠EDB=∠B, ∴DE=EB;
(2)、解:ED=EB, 理由如下:取AB的中点O,连接CO、EO,
∵∠ACB=90°,∠ABC=30°, ∴∠A=60°,OC=OA, ∴△ACO为等边三角形, ∴CA=CO,
∵△CDE是等边三角形, ∴∠ACD=∠OCE,∴△ACD≌△OCE, ∴∠COE=∠A=60°,∴∠BOE=60°, ∴△COE≌△BOE, ∴EC=EB, ∴ED=EB;
(3)、取AB的中点O,连接CO、EO、EB, 由(2)得△ACD≌△OCE,
∴∠COE=∠A=60°,∴∠BOE=60°,△COE≌△BOE,∴EC=EB,∴ED=EB, ∵EH⊥AB,
∴DH=BH=3,∵GE∥AB, ∴∠G=180°﹣∠A=120°, ∴△CEG≌△DCO, ∴CG=OD,
设CG=a,则AG=5a,OD=a,∴AC=OC=4a,∵OC=OB, ∴4a=a+3+3, 解得,a=2,
即CG=2.


科目:初中数学 来源: 题型:
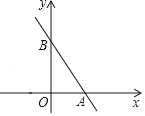
【题目】如图,直线l的解析式为y=﹣![]() x+b,它与坐标轴分别交于A、B两点,其中点B坐标为(0,4).
x+b,它与坐标轴分别交于A、B两点,其中点B坐标为(0,4).
(1)求出A点的坐标;
(2)在第一象限的角平分线上是否存在点Q使得∠QBA=90°?若存在,求点Q的坐标;若不存在,请说明理由.
(3)动点C从y轴上的点(0,10)出发,以每秒1cm的速度向负半轴运动,求出点C运动所有的时间t,使得△ABC为轴对称图形(直接写答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x的图象与二次函数y=﹣x2+3x图象的对称轴交于点B.
(1)写出点B的坐标;
(2)已知点P是二次函数y=﹣x2+3x图象在y轴右侧部分上的一个动点,将直线y=﹣2x沿y轴向上平移,分别交x轴、y轴于C、D两点.若以CD为直角边的△PCD与△OCD相似,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克) | ﹣4 | ﹣2 | 0 | 1 | 3 | 6 |
个数 | 10 | 13 | 30 | 25 | 15 | 7 |
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段统计如下:
学业考试体育成绩(分数段)统计表 | ||
分数段 | 人数(人) | 频率 |
A | 48 | 0.2 |
B | a | 0.25 |
C | 84 | 0.35 |
D | 36 | b |
E | 12 | 0.05 |
分数段为:(A:50分;B:49﹣45分;C:44﹣40分;D:39﹣30分;E:29﹣0分) 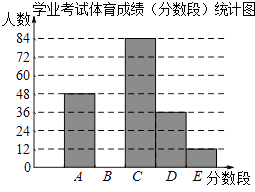
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 , b的值为 ,
(2)将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(3)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”请问:甲同学的体育成绩应在什么分数段内?(填相应分数段的字母)
(4)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:定义一种新运算“⊙”:
1⊙3=1×4+3=7,3⊙﹣1=3×4﹣1=11,5⊙4=5×4+4=24
4⊙(﹣3)=4×4﹣3=13,(﹣2)⊙(﹣5)=(﹣2)×4﹣5=﹣13,……
(1)写出一般结论:a⊙b=_____;
(2)如果a≠b,那么a⊙b_____b⊙a(填“=”或“≠”)
(3)先化简,再求值:(a﹣b)⊙(2a+3b).其中a=﹣![]() ,b=2019.
,b=2019.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com