
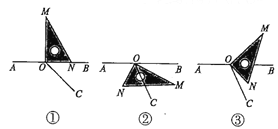
【题目】如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90![]() ).
).
(1)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由;
(2)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=60![]() ,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
【答案】(1)ON平分∠AOC (2)∠BOM=∠NOC+30°
【解析】试题分析:(1)由角平分线的定义可知∠BOM=∠MOC,由∠NOM=90°,可知∠BOM+∠AON=90°,∠MOC+∠NOC=90°,根据等角的余角相等可知∠AON=∠NOC;
(2)根据题意可知∠NOC+∠NOB=60°,∠BOM+∠NOB=90°,由∠BOM=90°﹣∠NOB、∠BON=60°﹣∠NOC可得到∠BOM=∠NOC+30°.
试题解析:解:(1)ON平分∠AOC.理由如下:
∵OM平分∠BOC,∴∠BOM=∠MOC.
∵∠MON=90°,∴∠BOM+∠AON=90°.
又∵∠MOC+∠NOC=90°
∴∠AON=∠NOC,即ON平分∠AOC.
(2)∠BOM=∠NOC+30°.理由如下:
∵∠BOC=60°,即:∠NOC+∠NOB=60°,又因为∠BOM+∠NOB=90°,所以:∠BOM=90°﹣∠NOB=90°﹣(60°﹣∠NOC)=∠NOC+30°,∴∠BOM与∠NOC之间存在的数量关系是:∠BOM=∠NOC+30°.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°. 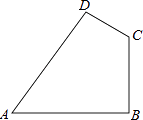
(1)猜想的∠A与∠C关系;
(2)求出四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A校女生占全校总人数的40%,B校女生占全校总人数的55%,则女生人数( )
A.A校多于B校
B.A校与B校一样多
C.A校少于B校
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断正误,并说明理由
(1)给定一组数据,那么这组数据的众数有可能不唯一;理由
(2)给定一组数据,那么这组数据的平均数一定是这组数据中的一个数;
理由
(3)n个数的中位数一定是这n个数中的某一个;理由
(4)求9个数据(x1、x2、……、x9 , 其平均数为m)的标准差S, 计算公式为: ![]() ;理由
;理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在各地区基本普及使用,某市一商场为响应号召,推广销售,该商场计划用3800元购进两种节能灯共120只,这两种节能灯的进价、售价如下表:

(1)求甲、乙两种型号节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com