
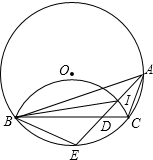
 如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.
如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.分析 (1)根据已知条件即可得到结论;
(2)根据相似三角形的性质得到$\frac{AB}{BD}=\frac{AE}{BE}$,∠BAE=∠DBE,由角平分线的性质得到∠ABI=∠DBI,根据等式的性质得到∠EBI=∠EIB,根据等腰三角形的判定定理得到BE=EI,等量代换即可得到结论;
(3)如图2,易证过点I的$\widehat{BC}$的半径为BE,根据勾股定理可以求出BE、DE的长,再根据BE2=AE•DE就可求出AD的长.
解答 (1)证明:∵EB2=ED•EA,
∴$\frac{EB}{EA}=\frac{DE}{EB}$,
∵∠E=∠E,
∴△ABE∽△BDE;
(2)证明:∵△ABE∽△BDE,
∴$\frac{AB}{BD}=\frac{AE}{BE}$,∠BAE=∠DBE,
∵BI平分∠ABC,
∴∠ABI=∠DBI,
∵∠EBI=∠EBD+∠DBI,∠BIE=∠BAD+∠ABI,
∴∠EBI=∠EIB,
∴BE=EI,
∴$\frac{AB}{BD}$=$\frac{AE}{EI}$;
(3)解:连接EC、OB、OC、OE,设OE交BC于F,如图,
∵∠BAE=∠EBC,∠EBC=∠EAC,
∴∠BAE=∠EAC,
∵∠BOE=2∠BAE,∠COE=2∠CAE,
∴∠BOE=∠COE,
∴$\widehat{BE}$=$\widehat{CE}$,
∴EB=EC,
∴EB=EC=EI,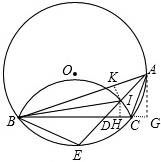
∴点E是过点I的$\widehat{BC}$的圆心,EB是过点I的$\widehat{BC}$的半径,
∵OB=OC,∠BOE=∠COE,
∴BF=CF=$\frac{1}{2}$BC=4,
在Rt△OFC中,
∵OC=5,FC=4,
∴OF=3,
∴EF=OE-OF=5-3=2,
∴BE=$\sqrt{B{F}^{2}+E{F}^{2}}$=2$\sqrt{5}$,
∵∠BDE=45°,∠DFE=90°,
∴∠DEF=90°-45°=45°=∠FDE,
∴DF=EF=2,
∴BD=BF+DF=4+2=6,DE=2$\sqrt{2}$,
∵AE•DE=BE2,
∴(AD+2$\sqrt{2}$)×2$\sqrt{2}$=(2$\sqrt{5}$)2,
∴AD=3$\sqrt{2}$.
点评 本题考查了弧与圆心角及弦的关系、相似三角形的判定和性质、圆周角定理、三角函数的定义、等腰三角形的判定与性质、三角形的外角性质、角平分线的性质、勾股定理等知识,有一定的综合性.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,如图,在△ABC中,AB=AC,以AC为直径作⊙O分别交AC,BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:
已知,如图,在△ABC中,AB=AC,以AC为直径作⊙O分别交AC,BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A、B两地相距80km,甲、乙二人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DB、OC分别表示表示甲、乙二人离开A地距离S(km)与时间t(h)的函数关系,根据题中的图象填空:
已知A、B两地相距80km,甲、乙二人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DB、OC分别表示表示甲、乙二人离开A地距离S(km)与时间t(h)的函数关系,根据题中的图象填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角45°,他在二楼窗台B处测得M的仰角31°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度(结果保留两位小数)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角45°,他在二楼窗台B处测得M的仰角31°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度(结果保留两位小数)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com