
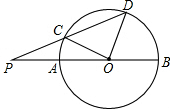
 如图,已知直径BA与弦DC的延长线交于点P,且PC=CO,$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,求∠DOB的度数.
如图,已知直径BA与弦DC的延长线交于点P,且PC=CO,$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,求∠DOB的度数. 分析 根据$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,得到∠COD=∠AOC+∠BOD=$\frac{1}{2}$×180°=90°,根据等腰三角形的性质得到∠OCD=∠D=45°,根据外角的性质得到∠P=∠COP=$\frac{1}{2}$∠DCO=22.5°,即可得到结论.
解答 解:∵$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,
∴∠COD=∠AOC+∠BOD=$\frac{1}{2}$×180°=90°,
∵OD=OC,
∴∠OCD=∠D=45°,
∵PC=CO,
∴∠P=∠COP=$\frac{1}{2}$∠DCO=22.5°,
∴∠DOB=∠P+∠D=67.5°.
点评 本题主要考查了圆心角、弧、弦的关系,三角形的外角的性质和等腰三角形的性质,正确理解同圆的半径相等是解题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕点D按顺时针方向旋转60°后得到△ECD,若AB=3,AC=2.
如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕点D按顺时针方向旋转60°后得到△ECD,若AB=3,AC=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
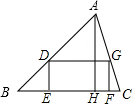 如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com