
【题目】已知数轴上有两点A、B,点A对应的数是40,点B对应的数是![]() .
.
![]() 求线段AB的长.
求线段AB的长.
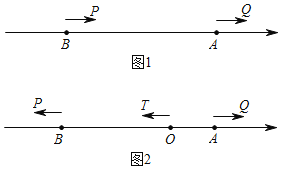
![]() 如图2,O表示原点,动点P、T分别从B、O两点同时出发向左运动,同时动点Q从点A出发向右运动,点P、T、Q的速度分别为5个单位长度
如图2,O表示原点,动点P、T分别从B、O两点同时出发向左运动,同时动点Q从点A出发向右运动,点P、T、Q的速度分别为5个单位长度![]() 秒、1个单位长度
秒、1个单位长度![]() 秒、2个单位长度
秒、2个单位长度![]() 秒,设运动时间为t.
秒,设运动时间为t.
![]() 求点P、T、Q表示的数
求点P、T、Q表示的数![]() 用含有t的代数式表示
用含有t的代数式表示![]() ;
;
![]() 在运动过程中,如果点M为线段PT的中点,点N为线段OQ的中点,试说明在运动过程中等量关系
在运动过程中,如果点M为线段PT的中点,点N为线段OQ的中点,试说明在运动过程中等量关系![]() 始终成立.
始终成立.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了调查某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 9 |
户数 | 3 | 4 | 2 | 1 |
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A.中位数是5吨
B.众数是5吨
C.极差是3吨
D.平均数是5.3吨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:﹣3﹣(﹣4)+7;
(2)计算:![]() ;
;
(3)计算:![]() ;
;
(4)计算:﹣14﹣(﹣2)2+6×(﹣![]() );
);
(5)化简:3x2+5x﹣5x2+3x;
(6)化简:6(m2﹣n)﹣3(n+2m2).
查看答案和解析>>
科目:初中数学 来源: 题型:
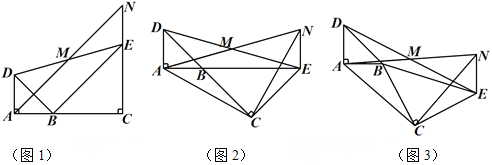
【题目】如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中点A(2,0),点P在射线 ![]() (x<0)上运动,设点P的横坐标为a,以AP为直径作⊙C,连接OP、PB,过点P作PQ⊥OP交⊙C于点Q.
(x<0)上运动,设点P的横坐标为a,以AP为直径作⊙C,连接OP、PB,过点P作PQ⊥OP交⊙C于点Q.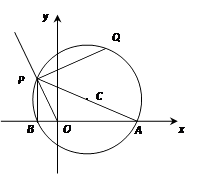
(1)证明:∠AOP=∠BPQ;
(2)当点P在运动的过程中,线段PQ的长度是否发生变化,若变化,请用含a的代数式表示PQ的长;若不变,求出PQ的长;
(3)当tan∠APO= ![]() 时,①求点Q坐标;②点D是圆上任意一点,求QD+
时,①求点Q坐标;②点D是圆上任意一点,求QD+ ![]() OD的最小值.
OD的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.
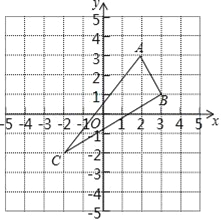
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).
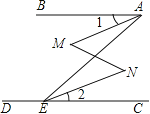
解:∵∠BAE+∠AED=180°(已知)
∴ ∥ (同旁内角互补,两直线平行)
∴∠BAE= (两直线平行,内错角相等)
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣
即∠MAE=
∴ ∥ (内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A、B两点在数轴上对应的数分别为﹣12和4.
(1)直接写出A、B两点之间的距离;
(2)若在数轴上存在一点P,使得AP=![]() PB,求点P表示的数.
PB,求点P表示的数.

(3)如图2,现有动点P、Q,若点P从点A出发,以每秒5个单位长度的速度沿数轴向右运动,同时点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动,求:当OP=4OQ时的运动时间t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,第n个三角形的以An为顶点的内角的度数为( )
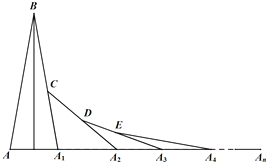
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com