
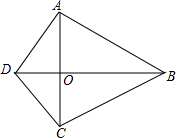
 已知:如图,四边形ABCD中,AB=CB=40,AD=CD=30.
已知:如图,四边形ABCD中,AB=CB=40,AD=CD=30.科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 46 | B. | 51 | C. | 61 | D. | 76 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 ”可以得到美丽的“中国结”图案,左边四个图案是由“
”可以得到美丽的“中国结”图案,左边四个图案是由“ ”平移后得到的类似“中国结”的图案,按图中规律,第10个图案中,小菱形“
”平移后得到的类似“中国结”的图案,按图中规律,第10个图案中,小菱形“ ”的个数200.
”的个数200.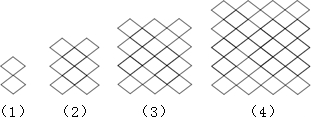
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
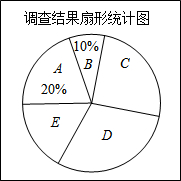 从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.| 组别 | 观点 | 频数(人数) |
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 | m |
| C | 汽车尾气排放 | n |
| D | 工厂造成污染 | 120 |
| E | 其他 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
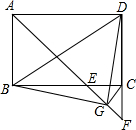 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com