
【题目】如图,已知△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.
求证:AE2+BF2=EF2.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】疫情期间,为满足口罩需求,某商店决定购进A,B两种口罩。若购进A口罩10盒,B口罩5盒,需要1000元。若购进A口罩4盒,B口罩3盒,需要550元.
(1)求A,B两种口罩每盒需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种口罩,考虑到市场需求,要求购进A口罩的数量不少于B口罩数量的6倍,且不超过B口罩数量的8倍,那么该商店共有几种进货方案?
(3)若销售每盒A口罩可以获利润20元,每盒B口罩可以获利润30元,在(2)的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(数学实验)如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干个可以拼出一些长方形来解释某些等式.例如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.

(初步运用)
(1)仿照例子,图③可以解释为: ;
(2)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+3b)、(a+5b),不画图形,试通过计算说明需要C类卡片多少张;
(拓展运用)
若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积为2a2+5ab+3b2,通过操作你会发现拼成的长方形的长宽分别是 ,将2a2+5ab+3b2改写成几个整式积的形式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
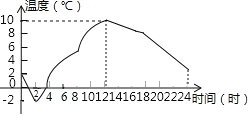
【题目】如图是某地某一天的气温随时间的变化而变化的图象,请根据图象回答:
(1)这一天什么时候气温最低?最低气温是多少?什么时候气温最高?最高气温是多少?
(2)求这一天的最大温差是多少?
(3)请你描述一下这一天气温随时间的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题.
(1)在正方形网格中,每个小正方形的边长均为1个单位长度,![]() 的三个顶点的位置如图所示,现将
的三个顶点的位置如图所示,现将![]() 平移,点
平移,点![]() 平移到点
平移到点![]() 的位置,
的位置,![]() 、
、![]() 点平移后的对应点分别是
点平移后的对应点分别是![]() 、
、![]() .
.
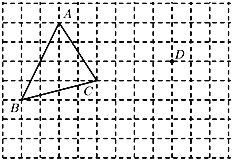
①画出平移后的![]() .
.
②连接![]() 、
、![]() ,则这两条线段之间的关系是__________.
,则这两条线段之间的关系是__________.
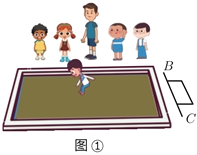
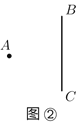
(2)如图①是体育课上跳远的场景,若运动员落地时后脚跟所在的点为![]() ,起跳线为
,起跳线为![]() ,请用图②说明怎样测量该运动员的跳远成绩,并说明其中的原因.
,请用图②说明怎样测量该运动员的跳远成绩,并说明其中的原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AEM=∠DFN=a,∠EMN=∠MNF=b,∠PEM=![]() ∠AEM,∠MNP=
∠AEM,∠MNP=![]() ∠FNP,∠BEP,∠NFD的角平分线交于点I,若∠I=∠P,则a和b的数量关系为_____(用含a的式子表示b).
∠FNP,∠BEP,∠NFD的角平分线交于点I,若∠I=∠P,则a和b的数量关系为_____(用含a的式子表示b).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com